Hình trụ. Diện tích xung quanh và thể tích hình trụ
Lý thuyết về Hình trụ. Diện tích xung quanh và thể tích hình trụ
1. Khái niệm hình trụ
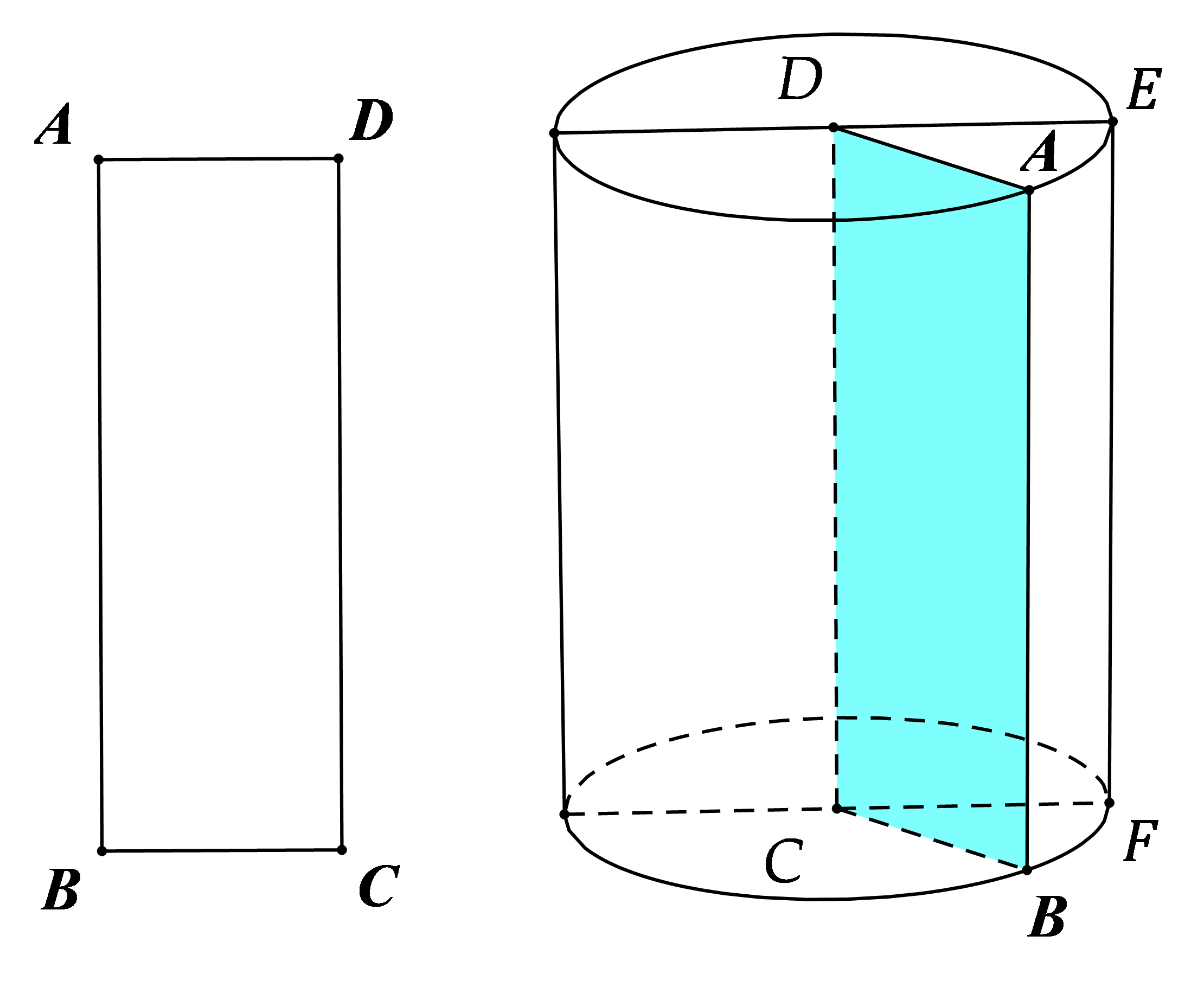
Khi quay hình chữ nhật $ABCD$ một vòng quanh cạnh $CD$ cố định ta thu được một hình trụ
– Hai đáy là hình tròn bằng nhau và nằm trên hai mặt phẳng song song.
– $DC$ là trục của hình trụ.
– Các đường sinh của hình trụ( chẳng hạn $EF$) vuông góc với hai mặt đáy.
Độ dài đường sinh cũng là độ dài đường cao của hình trụ.
2. Diện tích xung quanh, toàn phần của hình trụ
\[{S_{xq}} = 2\pi rh\]
– Diện tích toàn phần của hình trụ: \[{S_{tp}} = 2\pi rh + 2\pi {r^2}\]
($r$: là bán kính đường tròn đáy, $h$ là chiều cao)
3. Thể tích hình trụ
Công thức tính thể tích hình trụ: \[V = Sh = \pi {r^2}h\]
($S$ là diện tích đáy, $h$: là chiều cao)
Bài tập tự luyện có đáp án
Câu 1: Cho hình trụ có bán kính đáy $ r=4\,\left( cm \right) $ và chiều cao $ h=5\,\left( cm \right) $ . Diện tích xung quanh của hình trụ là
- A
- B
- C
- D
Diện tích xung quanh của hình trụ là $ {{S}_{xq}}=2\pi rh=2\pi .4.5=40\pi \,\,\left( c{{m}^{2}} \right) $
Câu 2: Cho hình trụ có chu vi đáy là $ 8\pi $ và chiều cao $ h=10 $ . Tính thể tích hình trụ.
- A
- B
- C
- D
Ta có chu vi đáy $ C=2\pi R=8\pi \Rightarrow R=4 $
Thể tích hình trụ là $ V=\pi {{R}^{2}}h=\pi {{.4}^{2}}.10=160\pi $ (đvtt).
Câu 3: Hình trụ có bán kính đáy $ r $ và chiều cao $ h $ có thể tích là:
- A
- B
- C
- D
Thể tích hình trụ có bán kính đáy $ r $ và chiều cao $ h $ là $ V=\pi {{r}^{2}}h $
Câu 4: Tính chiều cao của hình trụ có diện tích toàn phần gấp đôi diện tích xung quanh và bán kính đáy là $ 3\,cm $ .
- A
- B
- C
- D
Từ giả thiết ta có $ 2\pi Rh+2\pi {{R}^{2}}=2.2.\pi Rh\Rightarrow Rh={{R}^{2}}\Rightarrow R=h $
Vậy chiều cao của hình trụ là $ 3\,cm $ .
Câu 5: Một cái đèn có phần lồng đèn hình trụ (không phủ hai đáy) với bán kính $ 8cm $ và chiều cao $ 30cm. $ Để trang trí phần lồng đèn đó người ta cần sử dụng một tấm vải hình chữ nhật có kích thước như thế nào?
- A
- B
- C
- D
Miếng vải hình chữ nhật có một cạnh là chiều cao hình trụ, một cạnh là chu vi đáy hình trụ.
Chu vi đáy hình trụ là: \[ 2\pi .r=2\pi .8=16\pi \,\left( cm \right) \] .
Vì \[ 16\pi > 30 \] nên tấm vải có chiều rộng \[ 30cm, \]chiều dài \[16\pi \]
Câu 6: Cho hình trụ có bán kính đáy $ R=3\,(cm) $ và chiều cao $ h=6\,(cm) $ . Diện tích xung quanh của hình trụ là.
- A
- B
- C
- D
Diện tích xung quanh của hình trụ là $ {{S}_{xq}}=2\pi Rh=2\pi .3.6=36\pi (c{{m}^{2}}) $ .
Câu 7: Cho hình trụ có bán kính đáy $ R=8\,\,(cm) $ và diện tích toàn phần $ 564\pi \,\,(c{{m}^{2}}) $ . Tính chiều cao của hình trụ.
- A
- B
- C
- D
Ta có diện tích toàn phần của hình trụ $ {{S}_{tp}}={{S}_{xq}}+{{S}_{2d}}=2\pi Rh+2\pi {{R}^{2}}=564\pi $
$ \Leftrightarrow 16\pi h+2\pi {{.8}^{2}}=564\pi \Rightarrow h=27,25cm $ .
Câu 8: Cho hình trụ có bán kính đáy $ R=4\,(cm) $ và chiều cao $ h=5\,\,(cm) $ . Diện tích xung quanh của hình trụ là.
- A
- B
- C
- D
Diện tích xung quanh của hình trụ là $ {{S}_{xq}}=2\pi Rh=2\pi .4.5=40\pi (c{{m}^{2}}) $ .
Câu 9: Một hình trụ có bán kính bằng $ 2,5cm, $ diện tích xung quanh bằng $ 25\pi \,c{{m}^{2}} $ . Khi đó, diện tích toàn phần của hình trụ là:
- A
- B
- C
- D
Diện tích toàn phần của hình trụ là: $ {{S}_{tp}}={{S}_{xq}}+{{S}_{2d}}={{S}_{xq}}+2\pi {{r}^{2}} $
Suy ra $ {{S}_{tp}}=25\pi +2\pi .2,{{5}^{2}}=37,5\pi \left( c{{m}^{2}} \right). $
Câu 10: Cho hình trụ có chu vi đáy là $ 8\pi $ và chiều cao $ h=10 $ . Tính thể tích hình trụ.
- A
- B
- C
- D
Ta có chu vi đáy $ C=2\pi r=8\pi \Rightarrow r=4 $
Thể tích hình trụ là $ V=\pi {{r}^{2}}h=\pi {{.4}^{2}}.10=160\pi $ (đvtt).
Câu 11: Chọn câu đúng. Cho hình trụ có bán kính đáy $ R $ và chiều cao $ h $ . Nếu ta tăng chiều cao lên hai lần và giảm bán kính đáy đi hai lần thì.
- A
- B
- C
- D
Chiều cao mới của hình trụ là $ {h}'=2h $ ; bán kính đáy mới là $ {R}'=\dfrac{R}{2} $
Hình trụ mới có :
Chu vi đáy $ 2\pi {R}'=2\pi \dfrac{R}{2}=\pi R < 2\pi R=C $
Diện tích toàn phần $ 2\pi {R}'h+2\pi {{R}^{\prime 2}}=2\pi Rh+\dfrac{\pi {{R}^{2}}}{2}\ne 2\pi Rh+2\pi {{R}^{2}} $
Thể tích $ \pi {{R}^{\prime 2}}h=\dfrac{\pi {{R}^{2}}h}{2}\ne \pi {{R}^{2}}h $
Diện tích xung quanh $ 2\pi {R}'h=2\pi .\dfrac{R}{2}.2h=2\pi Rh $ .
Câu 12: Một lon sữa đầy chứa được $ 650ml $ sữa. Biết rằng chiều cao của lon sữa là $ 1dm. $ Diện tích đáy của lon sữa là:
- A
- B
- C
- D
Đổi $ 1dm=10cm,\,\,650ml=650\,c{{m}^{3}}. $
Ta có: $ V=S.h $ (V là thể tích, S là diện tích đáy, h là chiều cao)
Suy ra diện tích đáy của lon sữa là: $ S=\dfrac{V}{h}=\dfrac{650}{10}=65\left( c{{m}^{2}} \right). $
Câu 13: Cho hình trụ có bán kính đáy $ R=12\,\,(cm) $ và diện tích toàn phần $ 672\pi \,\,(c{{m}^{2}}) $ . Tính chiều cao của hình trụ.
- A
- B
- C
- D
Ta có diện tích toàn phần của hình trụ $ \Leftrightarrow 24\pi h+2\pi {{.12}^{2}}=672\pi \Rightarrow h=16cm $ .
Câu 14: Khi quay hình chữ nhật $ ABCD $ một vòng quanh cạnh $ AB $ cố định thì được hình trụ có trục là:
- A
- B
- C
- D
Khi quay hình chữ nhật $ ABCD $ một vòng quanh cạnh $ AB $ cố định thì được hình trụ có trục là $ AB $ .
Câu 15: Cắt hình trụ bởi mặt phẳng song song với đáy thì mặt cắt là:
- A
- B
- C
- D
Cắt hình trụ bởi mặt phẳng song song với đáy thì mặt cắt là hình tròn bằng hình tròn đáy hay hình tròn có bán kính bằng bán kính đáy.