Hệ số góc của đường thẳng y = ax + b (a ≠ 0)
Lý thuyết về Hệ số góc của đường thẳng y = ax + b (a ≠ 0)
1. Góc tạo bởi đường thẳng y = ax + b (a ≠ 0) và trục Ox
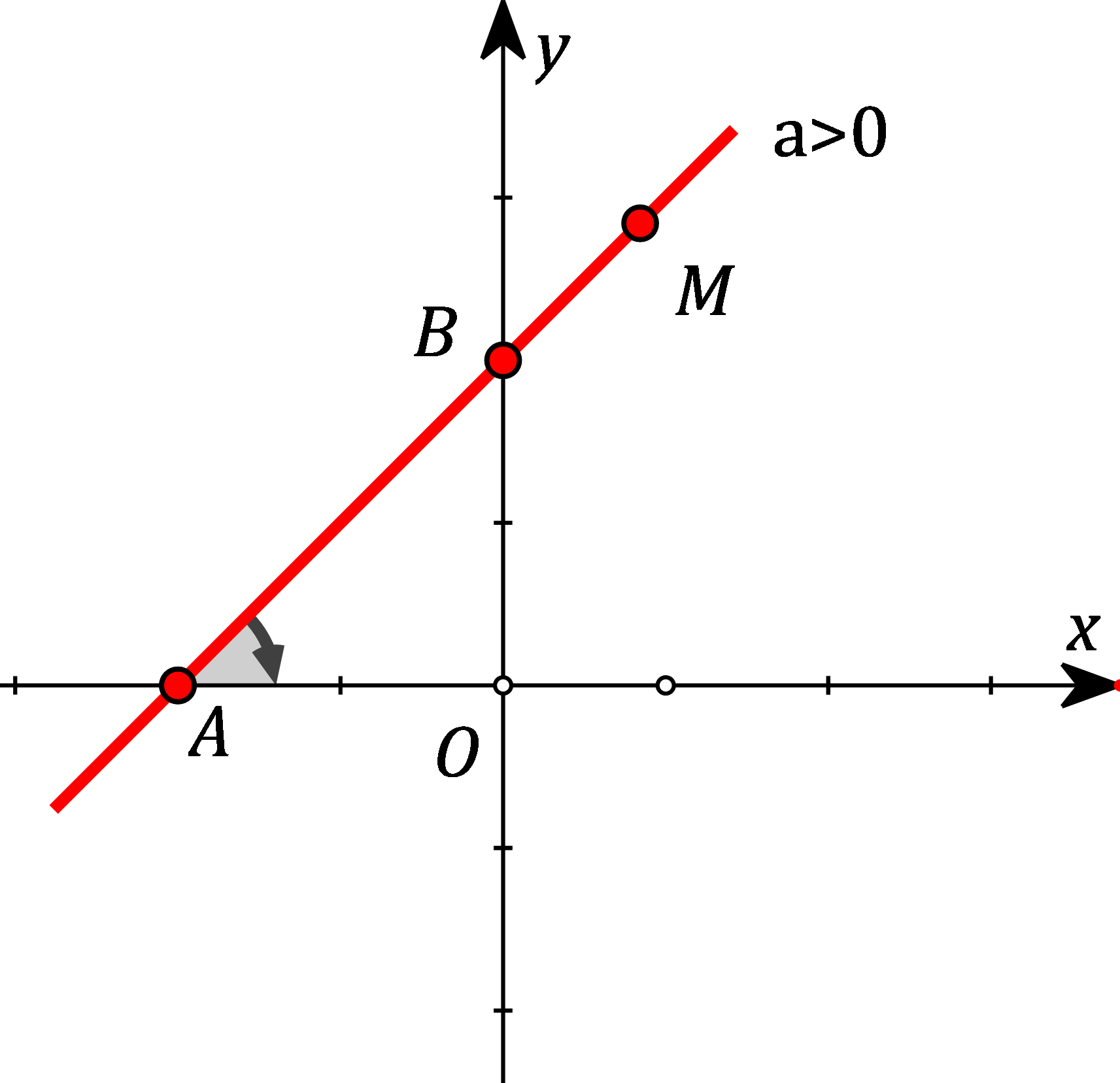
Gọi A là giao điểm của đường thẳng y=ax+b với Ox và M là một điểm thuộc đường thẳng, nằm phía trên trục Ox. Khi đó góc ^MAx được gọi là góc tạo bởi đường thẳng y=ax+b và trục Ox.
2. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)
Khi a>0, góc tạo bởi đường thẳng y=ax+b và trục Ox là góc nhọn và nếu a càng lớn thì góc đó càng lớn.
Khi a<0, góc tạo bởi đường thẳng y=ax+b và trục Ox là góc tù và nếu a càng bé thì góc đó càng lớn.
Như vậy, góc tạo bởi đường thẳng y=ax+b và trục Ox phụ thuộc vào a.
Người ta gọi a là hệ số góc của đường thẳng y=ax+b.
Lưu ý: Khi a>0, ta có tan^MAX=OBOA=|b||−ba|=|a|=a
Từ đó dùng bảng lượng giác hoặc máy tính bỏ túi suy ra số đo của ^MAX
Khi a<0, ta có tan(1800−^MAX)=tan^OAB=OBOA=|b||−ba|=|a|=−a
Từ đó tìm được số đo của góc (1800−^MAx) rồi suy ra số đo của góc ^MAx
Bài tập tự luyện có đáp án
Câu 1: Hệ số góc của đường thẳng d biết d đi qua điểm M(−3;2) và N(1;−1) là
- A
- B
- C
- D
Gọi d:y=ax+b(a≠0) đi qua 2 điểm M(−3;2) và N(1;−1)
M thuộc d⇔−3a+b=2⇒b=2+3a(1)
N thuộc d⇔1.a+b=−1⇔b=−1−a(2)
Từ (1) và (2) suy ra 2+3a=−1−a⇔4a=−3⇔a=−34
suy ra b=−1−a=−1+34=−14
Vậy d:y=−34x−14
Hệ số góc của d là k=−34 .
Câu 2: Tính góc tạo bởi tia Ox và đường thẳng y=√3x−6
- A
- B
- C
- D
Gọi α là góc tạo bởi tia Ox và đường thẳng d . Ta có tanα=√3⇒α=60∘
Câu 3: Góc tạo bởi tia Ox và đường thẳng y=1√3x+2 bằng
- A
- B
- C
- D
Gọi α là góc tạo bởi tia Ox và d . Ta có tanα=1√3⇒α=30∘ .
Câu 4: Góc tạo bởi đường thẳng (d):y=x+2020 với trục Ox bằng
- A
- B
- C
- D
Nếu α là góc tạo bởi đường thẳng (d):y=ax+b với trục Ox thì a=tanα .
Do đó ta có 1=tanα⇒α=45∘
Câu 5: Đường thẳng d có hệ số góc bằng 2 và đi qua điểm A(2;1) có phương trình là
- A
- B
- C
- D
Gọi phương trình đường thẳng d:y=ax+b
Vì d có hệ số góc bằng 2 nên a=2(tm)⇒y=2x+b
Thay tọa độ điểm A vào phương trình đường thẳng d ta có 2.2+b=1⇔b=−3
Nên d:y=2x−3 .
Câu 6: Đường thẳng d đi qua B(√3;−5) và tạo với trục Ox một góc bằng 60∘ có phương trình là
- A
- B
- C
- D
Gọi phương trình đường thẳng d:y=ax+b(a≠0)
Vì góc tạo bởi đường thẳng d và trục Ox là 60∘ nên
a=tan60∘=√3⇒y=√3x+b
Thay tọa độ điểm B vào phương trình đường thẳng d ta có √3.√3+b=−5⇒b=−8
Nên d:y=√3x−8 .
Câu 7: Tìm m biết đường thẳng d:y=(2m−4)x+5 song song với đường thẳng d′:2x−y−3=0
- A
- B
- C
- D
Ta có d song song với d′ nên hệ số góc của đường thẳng d là 2
Câu 8: Xác định các hệ số a,b của hàm số y=ax+b để đồ thị của nó đi qua hai điểm A(1;3)B(2;4)
- A
- B
- C
- D
Thay tọa độ A,B vào phương trình ta được
{3=a+b4=2a+b⇔{a=1b=2
Câu 9: Các điểm A(m;3) và B(1;m) nằm trên đường thẳng có hệ số góc m>0 và hệ số tự do là n. Tìm giá trị của m,n.
- A
- B
- C
- D
Đường thẳng y=mx+n đi qua điểm A(m;3) nên 3=m2+n . Đường thẳng y=mx+n đi qua điểm B(1;m) nên m=m+n . Từ đó n=0;m=√3
Câu 10: Hệ số góc của đường thẳng d biết d đi qua gốc tọa độ O và điểm M(1;3) là
- A
- B
- C
- D
Gọi phương trình đường thẳng d cần tìm là y=ax+b(a≠0)
Vì d đi qua gốc tọa độ nên b=0⇒y=ax
Thay tọa độ điểm M vào phương trình y=ax ta được 3=1.a⇒a=3 (TM)
Nên phương trình đường thẳng d:y=3x
Hệ số góc của d là k=3.
Câu 11: Đường thẳng d tạo với trục Ox một góc bằng 30∘ và cắt trục hoành tại điểm có hoành độ bằng 6 có phương trình là
- A
- B
- C
- D
Gọi phương trình đường thẳng d:y=ax+b(a≠0)
Vì góc tạo bởi đường thẳng d và trục Ox là 30∘
nên a=tan30∘=√33 ⇒y=√33x+b
Vì đường thẳng d cắt trục hoành tại điểm có hoành độ 6 nên d giao với trục hoành tại A(6;0)
Thay tọa độ điểm A vào phương trình đường thẳng d ta được √33.6+b=0⇒b=−2√3
Nên d:y=√33x−2√3 .
Câu 12: Viết phương trình đường thẳng d biết d có hệ số góc bằng -4 và đi qua điểm A(3;−2)
- A
- B
- C
- D
Gọi phương trình đường thẳng d:y=ax+b
Ta có phương trình đường thẳng d có hệ số góc bằng -4 nên a=−4
Thay điểm A(3;−2)⇒−2=3.(−4)+b⇔b=10
Câu 13: Cho đường thẳng d:y=(m+2)x−5 đi qua điểm có A(−1:2) . Hệ số góc của đường thẳng d là
- A
- B
- C
- D
Thay tọa độ điểm A vào phương trình đường thẳng d ta được (m+2).(−1)−5=2⇔−m−2=7⇔m=−9
Suy ra d:y=−7x−5
Hệ số góc của đường thẳng d là k=−7 .
Câu 14: Tìm hệ số góc của đường thẳng d biết d đi qua gốc tọa đồ O và điểm M(1;3)
- A
- B
- C
- D
Gọi phương trình đường thẳng d cần tìm là y=ax+b(a≠0)
Vì d đi qua gốc tọa độ nên b=0⇒y=ax
Thay tọa độ điểm M vào phương trình a=3
Nên hệ số góc của d là 3
Câu 15: Cho đường thẳng d:y=(2m−1)x+2√5 . Tính tanα với α là góc tạo bởi tia Ox và đường thẳng d biết d đi qua điểm A(1;2√5−√2) .
- A
- B
- C
- D
Thay x=1;y=2√5−√2 vào phương trình đường thẳng d ta được
(2m−1).1+2√5=2√5−√2⇔2m−1=−√2⇔m=1−√22
Gọi α là góc tạo bởi tia Ox và d . Ta có tanα=−√2.
Câu 16: Đường thẳng y=2(m+1)x−5m−8 đi qua điểm A(3;−5) có hệ số góc bằng bao nhiêu?
- A
- B
- C
- D
Thay tọa độ điểm A vào phương trình đường thẳng d ta có 2(m+1).3−5m−8=−5⇔m=−3
Khi đó y=−4x+7
Đường thẳng y=−4x+7 có hệ số góc k=−4 .
Câu 17: Tìm hệ số góc của đường thẳng x3+y2=1
- A
- B
- C
- D
Ta có y=−23x+2 Hệ số góc của đường thẳng −23
Câu 18: Cho đường thẳng d:y=(2m−3)x+m đi qua điểm có A(3;−1) . Hệ số góc của đường thẳng d là
- A
- B
- C
- D
Thay x=3;y=−1 vào phương trình đường thẳng d ta được (2m−3).3+m=−1⇔7m=8⇔m=87
Suy ra d:y=−57x+87
Hệ số góc của đường thẳng d là k=−57 .
Câu 19: Góc tạo bởi tia Ox và đường thẳng y=√3x−6 bằng
- A
- B
- C
- D
Gọi α là góc tạo bởi tia Ox và d . Ta có tanα=√3⇒α=60∘ .
Câu 20: Hệ số góc của đường thẳng d:y=(2m−4)x+5 biết nó song song với đường thẳng d′:2x−y−3=0 là
- A
- B
- C
- D
Xét d′:2x−y−3=0⇔y=2x−3 có hệ số góc là 2 . Mà d//d′ nên hệ số góc của d là 2 .
Câu 21: Đường thẳng d đi qua B(−1;1) và tạo với trục Ox một góc bằng 45∘ có phương trình là
- A
- B
- C
- D
Gọi phương trình đường thẳng d:y=ax+b(a≠0)
Vì góc tạo bởi đường thẳng d và trục Ox là 45∘ nên a=tan45∘=1⇒y=x+b
Thay tọa độ điểm B vào phương trình đường thẳng d ta có −1+b=1⇒b=2
Nên d:y=x+2 .
Câu 22: Hệ số góc của đường thẳng d:y=5mx+4m−1 biết nó song song với đường thẳng d′:x−3y+1=0 là
- A
- B
- C
- D
Xét d′:x−3y+1=0⇔y=13x+13 có hệ số góc là 13 . Mà d//d′ nên hệ số góc của d là 13 .
Câu 23: Cho đường thẳng d:y=(m+2)x−5 có hệ số góc là k=−4 . Giá trị m là
- A
- B
- C
- D
Hệ số góc của đường thẳng d là k=m+2(m≠−2)
Từ giả thiết suy ra m+2=−4⇔m=−6(TM) .
Câu 24: Cho đường thẳng (d):ax+(2a−1)y+3=0 . Biết (d) đi qua điểm M(1;−1) . Khi đó hệ số góc của đường thẳng (d) là
- A
- B
- C
- D
M∈(d)⇒a.1+(2a−1)(−1)+3=0⇔a=4
Khi đó (d):4x+7y+3=0⇒y=−47x−37
Vậy hệ số góc của đường thẳng (d) là: −47
Câu 25: Góc hợp bởi đường thẳng y=√3x−√32(d) và trục Ox là:
- A
- B
- C
- D
Gọi α là góc giữa (d) với chiều dương của truc Ox
Khi đó ta có tanα=√3⇒α=600
Vậy góc giữa (d) với truc Ox là 600
Câu 26: Góc hợp bởi đường thẳng y=−x−√3(d) và trục Ox là:
- A
- B
- C
- D
Gọi α là góc giữa (d) với chiều dương của truc Ox
Khi đó ta có tanα=−1⇒α=1350
Vậy góc giữa (d) với truc Ox là 1800−1350=450
Câu 27: Tìm m để hệ số góc của đường thẳng d:y=(3−m)x+2 vuông góc với đường thẳng d′:x−2y−6=0
- A
- B
- C
- D
Ta có: d′:x−2y−6=0⇔y=12x−3
Vì d⊥d′⇒(3−m).12=−1⇔3−m=−2⇔m=5
Vậy m=5 là giá trị cần tìm.
Câu 28: Cho đường thẳng y=m.x+√3 . Góc tạo bởi tia Ox và đường thẳng d biết d đi qua điểm A(3;0) bằng
- A
- B
- C
- D
Thay tọa độ điểm A vào phương trình đường thẳng d ta được
m.3+√3=0⇔m=−√33⇒d:y=−√33x+√3
Gọi α là góc tạo bởi tia Ox và d . Ta có tanα=−√33⇒α=150∘ .
Câu 29: Đường thẳng d có hệ số góc bằng −4 và đi qua điểm A(3;−2) có phương trình là
- A
- B
- C
- D
Gọi phương trình đường thẳng d:y=ax+b
Vì d có hệ số góc bằng −4 nên a=−4⇒y=−4x+b
Thay tọa độ điểm A vào phương trình đường thẳng d ta có −4.3+b=−2⇒b=10 Nên d:y=−4x+10 .
Câu 30: Đường thẳng y=ax+5 đi qua điểm M(−1;3) thì hệ số góc của nó bằng:
- A
- B
- C
- D
Thay điểm M(−1;3) ta có phương trình 3=−a+5⇒a=2 .
Hệ số góc của đường thẳng y=ax+5 bằng 2
Câu 31: Xác định tham số m biết d:y=(3−m)x+1 vuông góc với đường thẳng d′:x−2y−6=0
- A
- B
- C
- D
Ta có d′:x−2y−6=0 ⇔y=12x−3
Vì d⊥d′⇒(3−m).12=−1⇔3−m=−2⇔m=5