Các công thức tính nhanh cực trị hàm trùng phương y=ax4+bx2+c
Lý thuyết về Các công thức tính nhanh cực trị hàm trùng phương y=ax4+bx2+c
Xét hàm số y=ax4+bx2+c.
- Hàm có có một cực trị khi {ab⩾0a2+b2≠0.
- Hàm số có ba cực trị khi ab<0.
Khi hàm số có ba điểm cực trị −x1=−√−b2a<0<x1=√−b2a (là ba nghiệm của phương trình y′=0) tương ứng với ba điểm cực trị B;A;C của đồ thị hàm số.
- Khi a>0 thì x=±x1 là các điểm cực tiểu của hàm số, x=0 là điểm cực đại của hàm số.
Khi a<0 thì x=±x1 là các điểm cực đại của hàm số, x=0 là điểm cực tiểu của hàm số.
- Bán kính đường tròn ngoại tiếp RABC=b3−8a8|a|b.
- Bán kính đường tròn nội tiếp rABC=b2|a|(1+√1−b3a).
- Diện tích tam giác SABC=√−b532a3.
- Góc ở đỉnh: cos^BAC=b3+8ab3−8a; cos^ABC=cos^ACB=√8a8a−b3.
- Tam giác ABC vuông (tại A) khi b3+8a=0.
- Tam giác ABC đều khi b3+24a=0.
- Phương trình hai cạnh AB,AC:y=±(√−b2a)3x+c.
Bài tập tự luyện có đáp án
Câu 1: Cho đồ thị hàm số y=ax4+bx2+c(a≠0) có ba điểm cực trị A,B,C phân biệt. Khẳng định nào sau đây luôn đúng?
- A
- B
- C
- D
Vì đồ thị hàm bậc 4 trùng phương luôn nhận trục Oy làm trục đối xứng nên các điểm cực trị tạo thành tam giác cân ⇒ΔABC cân.
Câu 2: Cho hàm số y=−x4−2mx2+2 . Với giá trị nào của m thì hàm số chỉ có cực đại mà không có cực tiểu?
- A
- B
- C
- D
Vì hệ số của x4 là bằng −1<0 nên để hàm số chỉ có cực đại mà không có cực tiểu khi và chỉ khi hàm số chỉ có 1 cực đại
hay phương trình y′=0 có nghiệm duy nhất.
Ta có:
y′=−4x3−4mx=0
⇔x(x2+m)=0 . Ta thấy phương trình luôn có nghiệm x=0.
Để phương trình y′=0 có nghiệm duy nhất.
* TH1: Phương trình x2+m=0 vô nghiệm ⇔m>0
* TH2: Phương trình x2−m=0 có nghiệm kép x=0 , suy ra m=0 .
Vậy m≥0
Câu 3: Giá trị của m để hàm số y=mx4+2x2−1 có ba điểm cực trị là:
- A
- B
- C
- D
Để hàm số có ba điểm cực trị ⇔2m<0⇔m<0
Vậy m<0 .
Câu 4: Cho hàm số y=x4+ax2+b . Biết rằng đồ thị hàm số nhận điểm A(−1;4) là điểm cực tiểu. Tổng 2a+b bằng:
- A
- B
- C
- D
Ta có y=x4+ax2+b⇒y′=4x3+2ax,∀x∈R .
Theo giả thiết, ta được
{y′(−1)=0y(−1)=4⇔{−4−2a=0a+b+1=4⇔{a=−2b=5⇒2a+b=1 .
Câu 5: Cho hàm số y=x4−(m−1)x2+m3+1(C) . Tìm m để đồ thị hàm số (C) không có cực đại
- A
- B
- C
- D
Vì hệ số của x4 là bằng 1>0 nên để hàm số không có cực đại khi và chỉ khi hàm số chỉ có 1 cực tiểu
hay phương trình y′=0 có nghiệm duy nhất.
Ta có:
y′=4x3−2(m−1)x=0
⇔x(2x2−m+1)=0 . Ta thấy phương trình luôn có nghiệm x=0 .
Để phương trình y′=0 có nghiệm duy nhất.
* TH1: Phương trình 2x2−m+1=0 vô nghiệm ⇔m<1
* TH2: Phương trình 2x2−m+1=0 có nghiệm kép x=0 , suy ra m=1 .
Vậy m≤1
Câu 6: Tìm m để hàm số y=−x4+(2m+1)x2+2 đạt cực đại tại x=2
- A
- B
- C
- D
y′=−4x3+2(2m+1)xy″=−12x2+4m+2
Để hàm số đại cực đại tại x=2 ⇔{y′(2)=0y″(2)<0⇔m=72
Câu 7: Cho hàm số y=mx4+(m2−9)x2+10 . Tìm m để hàm số có 3 điểm cực trị
- A
- B
- C
- D
Hàm số có 3 điểm cực trị ⇔m(m2−9)<0⇔[0<m<3m<−3
Câu 8: Giá trị của m để hàm số y=x4−2mx2 có một điểm cực trị là:
- A
- B
- C
- D
Để hàm số có một cực trị ⇔[2m<0m=0⇔m≤0
Câu 9: Cho hàm số y=mx4+(m−1)x2+m2−m+1(C) . Tìm m để đồ thị hàm số (C) chỉ có một cực trị
- A
- B
- C
- D
Ta có
y′=4mx3+2(m−1)x=2x(2mx2+m−1)⇒y′=0⇔[x=0g(x)=2mx2+m−1=0(2)
Để hàm số (C) có một cực trị ⇔g(x) vô nghiệm hoặc có nghiệm kép x=0 .
TH1: m=0 ⇒(2) vô nghiệm. Suy ra m=0 thỏa mãn.
TH2: m≠0 .
g(x)=0 vô nghiệm ⇔1−m2m<0⇔[m>1m<0
g(x)=0 có nghiệm kép x=0 ⇔m=1
Vậy [m≥1m≤0
Câu 10: Cho hàm số y=(m−1)x4+(m2−4)x2+1 . Điều kiện để đồ thị hàm số có 3 điểm cực trị là:
- A
- B
- C
- D
Để đồ thị hàm số đã cho có ba điểm cực trị (m−1)(m2−4)<0⇔[1<m<2m<−2
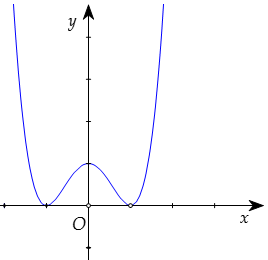
Câu 11:  Cho đồ thị hàm số y=ax4+bx2+c như hình vẽ.
Khẳng định nào sau đây là sai?
Cho đồ thị hàm số y=ax4+bx2+c như hình vẽ.
Khẳng định nào sau đây là sai?
 Cho đồ thị hàm số y=ax4+bx2+c như hình vẽ.
Khẳng định nào sau đây là sai?
Cho đồ thị hàm số y=ax4+bx2+c như hình vẽ.
Khẳng định nào sau đây là sai?- A
- B
- C
- D
Từ hình dạng đồ thị ta có a>0,c>0⇒Khẳng định “a<0 “ sai
y′=4ax3+2bx=0⇔[x=0x2=−b2a
Hàm số có ba cực trị nên −b2a>0⇔b<0
Xem thêm các bài tiếp theo bên dưới