Phương trình tiếp tuyến
Lý thuyết về Phương trình tiếp tuyến
1. Viết phương trình tiếp tuyến của đồ thị $\left( C \right):y=f\left( x \right)$ tại điểm $M\left( {{x}_{0}};{{y}_{0}} \right)$
PP giải:
B1: Tính đạo hàm ${y}'={f}'\left( x \right)$ suy ra hệ số góc tiếp tuyến $k={y}'\left( {{x}_{0}} \right)$
B2: Phương trình tiếp tuyến của đồ thị tại điểm $M\left( {{x}_{0}};{{y}_{0}} \right)$ có dạng $y={y}'\left( {{x}_{0}} \right)\left( x-{{x}_{0}} \right)+{{y}_{0}}$
Chú ý:
- Nếu đề cho hoành độ tiếp điểm ${{x}_{0}}$ thì tìm ${{y}_{0}}$ bằng cách thế vào hàm số ban đầu, tức ${{y}_{0}}=f\left( {{x}_{0}} \right)$.
- Nếu đề cho tung độ tiếp điểm ${{y}_{0}}$ thì tìm ${{x}_{0}}$ bằng cách giải phương trình $f\left( {{x}_{0}} \right)={{y}_{0}}$.
- Nếu đề bài yêu cầu viết phương trình tiếp tuyến tại các giao điểm của đồ thị hàm số $\left( C \right):y=f\left( x \right)$ và đường thẳng $d:y=ax+b$. Khi đó, các hoành độ tiếp điểm là nghiệm của phương trình hoành độ giao điểm giữa $\left( C \right):y=f\left( x \right)$ và $d:y=ax+b$.
2. Viết phương trình tiếp tuyến của đồ thị \[\left( C \right):y=f\left( x \right)\] biết hệ số góc \[k\]
PP giải:
- B1: Gọi \[M\left( {{x}_{0}};{{y}_{0}} \right)\] là tiếp điểm và tính \[{y}'={f}'\left( x \right)\]
- B2: Hệ số góc tiếp tuyến là \[k={y}'\left( {{x}_{0}} \right)\]
Giải phương trình này tìm được \[{{x}_{0}}\], thay vào hàm số ta được \[{{y}_{0}}\].
- B3: Với mỗi tiếp điểm ta tìm được các tiếp tuyến tương ứng \[d:y=k\left( x-{{x}_{0}} \right)+{{y}_{0}}\].
Chú ý: Đề bài thường cho hệ số góc tiếp tuyến dưới các dạng sau:
- Tiếp tuyến \[d\text{ // }\Delta :y=ax+b\Rightarrow \]hệ số góc của tiếp tuyến là \[k=a.\]
- Tiếp tuyến \[d\bot \Delta :y=ax+b\Rightarrow \] hệ số góc của tiếp tuyến là \[k=-\frac{1}{a}\cdot \]
- Tiếp tuyến tạo với trục hoành một góc \[\alpha \] thì hệ số góc của tiếp tuyến $d$ là \[k=\pm \tan \alpha .\]
3. Viết phương trình tiếp tuyến của đồ thị hàm số \[\left( C \right):y=f\left( x \right)\] biết tiếp tuyến đi qua \[A\left( {{x}_{A}};{{y}_{A}} \right).\]
Phương pháp giải
Cách 1.
- Bước 1: Phương trình tiếp tuyến đi qua \[A\left( {{x}_{A}};{{y}_{A}} \right)\] hệ số góc \[k\] có dạng:
\[d:y=k\left( x-{{x}_{A}} \right)+{{y}_{A}}\] \[(*)\]
- Bước 2: $d$ là tiếp tuyến của \[\left( C \right)\]khi và chỉ khi hệ sau có nghiệm:
\[\left\{ \begin{align}& f\left( x \right)=k\left( x-{{x}_{A}} \right)+{{y}_{A}} \\ & {f}'\left( x \right)=k \\ \end{align} \right.\].
- Bước 3: Giải hệ này tìm được $x$ suy ra $k$ và thế vào phương trình \[(*)\], ta được tiếp tuyến cần tìm.
Cách 2.
- Bước 1. Gọi \[M\left( {{x}_{0}};f\left( {{x}_{0}} \right) \right)\] là tiếp điểm và tính hệ số góc tiếp tuyến \[k={y}'\left( {{x}_{0}} \right)={f}'\left( {{x}_{0}} \right)\] theo \[{{x}_{0}}.\]
- Bước 2. Phương trình tiếp tuyến có dạng: \[d:y={y}'\left( {{x}_{0}} \right).\left( x-{{x}_{0}} \right)+{{y}_{0}}\] \[(**)\]
Do điểm \[A\left( {{x}_{A}};{{y}_{A}} \right)\in d\] nên \[{{y}_{A}}={y}'\left( {{x}_{0}} \right).\left( {{x}_{A}}-{{x}_{0}} \right)+{{y}_{0}}\]giải phương trình này sẽ tìm được \[{{x}_{0}}\].
- Bước 3. Thế \[{{x}_{0}}\] vào \[(**)\] ta được tiếp tuyến cần tìm.
Chú ý: Đối với dạng viết phương trình tiếp tuyến đi qua điểm việc tính toán tương đối mất thời gian.
4. Viết phương trình tiếp tuyến chung của hai đồ thị hàm số \[\left( {{C}_{1}} \right):y=f\left( x \right)\] và \[\left( {{C}_{2}} \right):y=g\left( x \right)\].
Phương pháp
- Bước 1. Gọi $d$ tiếp tuyến chung của $\left( {{C}_{1}} \right),\,\,\left( {{C}_{2}} \right)$ và ${{x}_{0}}$ là hoành độ tiếp điểm của $d$ và $\left( {{C}_{1}} \right)$ thì phương trình $d$ có dạng:
$y={f}'\left( {{x}_{0}} \right).\left( x-{{x}_{0}} \right)+f\left( {{x}_{0}} \right)$ $\left( *** \right)$
- Bước 2. Dùng điều kiện tiếp xúc của $d$ và $\left( {{C}_{2}} \right)$, tìm được ${{x}_{0}}$.
- Bước 3. Thế \[{{x}_{0}}\] vào $\left( *** \right)$ ta được tiếp tuyến cần tìm.
Bài tập tự luyện có đáp án
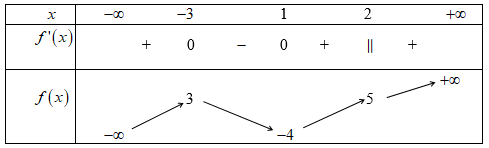
Câu 1: Cho hàm số $ y=f\left( x \right) $ có bảng biến thiên:
 Mệnh đề nào sau đây là đúng ?
Mệnh đề nào sau đây là đúng ?
 Mệnh đề nào sau đây là đúng ?
Mệnh đề nào sau đây là đúng ?- A
- B
- C
- D
Dựa vào bảng biến thiên ta thấy
Hàm số đồng biến trên các khoảng $ \left( -\infty ;-3 \right) $ và $ \left( 1;+\infty \right) $ .
Câu 2: Cho hàm số $ f(x) $ xác định trên $ \mathbb R \backslash \left\{ -1 \right\} $ , liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ. Hỏi mệnh đề nào dưới đây sai?


- A
- B
- C
- D
Từ bảng biến thiên ta thấy, hàm số không có tiệm cận ngang nên mệnh đề: "Đồ thị hàm số có tiệm cận ngang là $ y=-1 $ " là sai.
Dễ dàng thấy rằng các mệnh đề còn lại đúng.
Câu 3: Bảng biến thiên ở bên là của hàm số nào?


- A
- B
- C
- D
Từ bảng biến thiên ta thấy, đồ thị hàm số có tiệm cận đứng là $ x=-1 $ và tiệm cận ngang là $ y=2 $ $ \Rightarrow $ chọn phương án $ y=\dfrac{2x+1}{x+1} $
Câu 4: Cho hàm số $ y=f(x) $ có bảng biến thiên như sau:
 Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
 Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?- A
- B
- C
- D
Dựa vào bảng biến thiên hàm số trên, ta thấy hàm số nghịch biến trên các khoảng $ (-\infty ;0) $ và $ (2;+\infty ) $ .
Câu 5: Biết đồ thị hàm số $y=a{{x}^{3}}+b{{\text{x}}^{2}}+c\text{x}+d\left( a\ne 0 \right)$có dạng
 Trong các khẳng định, khẳng định đúng là
Trong các khẳng định, khẳng định đúng là
 Trong các khẳng định, khẳng định đúng là
Trong các khẳng định, khẳng định đúng là- A
- B
- C
- D
Trên tập xác định $\mathbb{R}$, ta thấy đồ thị hàm số đi xuống từ trái sang phải nên khẳng định ‘’Hàm số nghịch biến trên $\mathbb{R}$” đúng.
Câu 6: Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:
 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?- A
- B
- C
- D
Từ bảng biến thiên ta thấy $\underset{x\to \pm \infty }{\mathop{\lim }}\,f\left( x \right)=0,\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,=-\infty \Rightarrow $ Đồ thị hàm số nhận $y=0$ làm tiệm cận ngang, $x=0$ làm tiệm cận đứng và luôn nằm dưới trục hoành.
Câu 7: Bảng biến thiên sau là của hàm số nào?


- A
- B
- C
- D
Từ bảng biến thiên ta thấy, đồ thị hàm số có tiệm cận đứng là $ x=2 $ và tiệm cận ngang là $ y=1 $ $ \Rightarrow $ loại phương án $ y=\dfrac{x-1}{2x+1} $ và $ y=\dfrac{x+3}{2+x} $
Hàm số nghịch biến trên từng khoảng xác định $ \Rightarrow $ chọn phương án $ y=\dfrac{x+1}{x-2} $
Câu 8: Cho hàm số $ y=f\left( x \right) $ xác định và liên tục trên tập $ D=\mathbb R \backslash \left\{ -1 \right\} $ và có bảng biến thiên:
 Dựa vào bảng biến thiên của hàm số $ y=f\left( x \right) $ . Khẳng định nào sau đây là khẳng định sai?
Dựa vào bảng biến thiên của hàm số $ y=f\left( x \right) $ . Khẳng định nào sau đây là khẳng định sai?
 Dựa vào bảng biến thiên của hàm số $ y=f\left( x \right) $ . Khẳng định nào sau đây là khẳng định sai?
Dựa vào bảng biến thiên của hàm số $ y=f\left( x \right) $ . Khẳng định nào sau đây là khẳng định sai?- A
- B
- C
- D
Từ bảng biến thiên ta có thể thấy ngay hàm số không nghịch biến trên khoảng $ \left( -\infty ;3 \right) $ vì hàm số không xác định tại $ x=-1 $ .
Dễ thấy các phương án còn lại đều đúng.
Câu 9: Cho hàm số $ y=f(x) $ có bảng biến thiên như hình vẽ bên. Hàm số $ y=f(x) $ nghịch biến trên khoảng nào trong các khoảng sau đây?


- A
- B
- C
- D
Chọn đáp án $ (-1;\,\,0). $
Câu 10: Cho hàm số $ y=f\left( x \right) $ liên tục trên $ \mathbb R $ và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là sai?


- A
- B
- C
- D
Giá trị hàm số tiến tới $ +\infty $ nên không có giá trị lớn nhất.
Từ bảng biến thiên ta thấy các phương án còn lại đều đúng.
Xem thêm các bài tiếp theo bên dưới