Định lí Ta - let trong tam giác
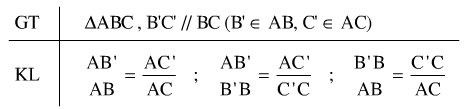
Lý thuyết về Định lí Ta - let trong tam giác
1. Tỉ số của hai đoạn thẳng
a) Định nghĩa:
– Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
– Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là $\dfrac{AB}{CD}$
b) Chú ý: Tỉ số của hai đoạn thẳng không phụ thuộc vào các chọn đơn vị đo.
c) Ví dụ: $AB = 10cm;CD = 4cm \Rightarrow \dfrac{{CD}}{{AB}} = \dfrac{4}{{10}} = \dfrac{2}{5}$
2. Đoạn thẳng tỉ lệ
Định nghĩa: Hai đoạn thẳng $AB$ và $CD$ gọi là tỉ lệ với hai đoạn thẳng $A’B’$ và $C’D’$ nếu có tỉ lệ thức
$\dfrac{AB}{CD}=\dfrac{{A}'{B}'}{{C}'{D}'}$ hay $\dfrac{AB}{{A}'{B}'}=\dfrac{CD}{{C}'{D}'}$
3. Định lí Talet trong tam giác
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lai thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Ví dụ: cho $B'C'//BC$ tính x theo hình vẽ
Ta có $B'C'//BC \Rightarrow \dfrac{{BB'}}{{AB}} = \dfrac{{CC'}}{{AC}} \Leftrightarrow \dfrac{2}{4} = \dfrac{x}{5} \Rightarrow x = \dfrac{{2.5}}{4} = \dfrac{5}{2}$
Bài tập tự luyện có đáp án
Câu 1: Cho tứ giác $ ABCD $ , lấy bất kỳ $ E\in BD $ . Qua $ E $ vẽ $ EF $ song song với $ AD $ ( $ F $ thuộc $ AB $ ), vẽ $ EG $ song song với DC ( $ G $ thuộc $ BC $ ). Chọn khẳng định sai.
- A
- B
- C
- D
Áp dụng định lí Ta-lét trong $ \Delta ABD $ với $ EF\text{//}AD $ , ta có $ \dfrac{BE}{ED}=\dfrac{BF}{FA} $ . (1)
Áp dụng định lí Ta-lét trong $ \Delta BDC $ với $ EG\text{//}DC $ , ta có $ \dfrac{BE}{ED}=\dfrac{BG}{GC} $ . (2)
Từ (1) và (2) suy ra $ \dfrac{BF}{FA}=\dfrac{BG}{GC} $ , do đó $ FG\text{//}AC $ (định lí Ta-lét đảo).
Câu 2: Chọn câu trả lời đúng. Cho hình bên, biết $ DE\text{//}AC $ , tìm x. 
- A
- B
- C
- D
Vì $ DE\text{//}AC $ , áp dụng định lý Talet, ta có:
$ \begin{array}{l} \dfrac{BD}{BA}=\dfrac{BE}{BC}\Rightarrow \dfrac{BD}{BD+DA}=\dfrac{BE}{BE+EC}\Rightarrow \dfrac{5}{5+2}=\dfrac{x}{x+2,5} \\ \Rightarrow \dfrac{x}{x+2,5}=\dfrac{5}{7}\Rightarrow 7x=5x+12,5\Rightarrow x=6,25. \end{array} $
Câu 3: Cho tam giác ABC; có MN//BC và độ dài các cạnh theo đơn vị (cm) như hình vẽ
 Giá trị của x thỏa mãn là
Giá trị của x thỏa mãn là
 Giá trị của x thỏa mãn là
Giá trị của x thỏa mãn là- A
- B
- C
- D
Ta có $ MN//BC\Rightarrow \dfrac{AM}{MB}=\dfrac{AN}{NC}\Leftrightarrow \dfrac{3}{4}=\dfrac{x}{20}\Rightarrow x=15cm $
Câu 4: Cho tam giác $ ABC $ có $ AB=9cm $ , điểm $ D $ thuộc cạnh $ AB $ sao cho $ AD=6cm $ . Kẻ $ DE $ song song với $ BC(E\in AC) $ , kẻ $ EF $ song song với $ CD(F\in AB) $ . Tính độ dài $ AF $ .
- A
- B
- C
- D

Áp dụng định lí Ta-lét :
Với $ \text{EF//}CD $ ta có $ \dfrac{AF}{AD}=\dfrac{AE}{AC} $ .
Với $ DE\text{//}BC $ ta có $ \dfrac{AE}{AC}=\dfrac{AD}{AB} $ .
Suy ra $ \dfrac{AF}{AD}=\dfrac{AD}{AB} $ , tức là $ \dfrac{AF}{6}=\dfrac{6}{9} $
Vậy AF = 4cm.
Câu 5: Tính độ dài $ x,y $ trong hình bên dưới. 
- A
- B
- C
- D
Áp dụng định lý Py-ta-go cho tam giác vuông $ O{A}'{B}' $ ta có:
$ \begin{array}{*{35}{l}} O{{A}^{\prime 2}}+{A}'{{B}^{\prime 2}}=O{{B}^{\prime 2}} \\ \Leftrightarrow {{2}^{2}}+{{4}^{2}}=O{{B}^{\prime 2}} \\ \Leftrightarrow O{{B}^{\prime 2}}=20 \\ \Rightarrow O{B}'=\sqrt{20} \end{array} $
$ {A}'{B}'\bot A{A}',\,AB\bot A{A}'\Rightarrow {A}'{B}'\text{//}AB $ (Theo định lý từ vuông góc đến song song)
Áp dụng định lý Ta-let, ta có:
$ \dfrac{O{A}'}{OA}=\dfrac{O{B}'}{OB}=\dfrac{{A}'{B}'}{AB} $ $ \Rightarrow \left\{ \begin{array}{l} \dfrac{\sqrt{20}}{x}=\dfrac{2}{5} \\ \dfrac{4}{y}=\dfrac{2}{5} \end{array} \right.\Leftrightarrow \left\{ \begin{array}{l} x=\dfrac{5.\sqrt{20}}{2}=5\sqrt{5} \\ y=\dfrac{4.5}{2}=10 \end{array} \right. $ Vậy $ x=5\sqrt{5} $ và $ y=10 $ .
Câu 6: Cho tam giác $ ABC $ , vuông tại B; có $ MN//BC $ và độ dài các cạnh theo đơn vị (cm) như hình vẽ
 Khi đó diện tích hình thang $ MNCB $ bằng
Khi đó diện tích hình thang $ MNCB $ bằng
 Khi đó diện tích hình thang $ MNCB $ bằng
Khi đó diện tích hình thang $ MNCB $ bằng- A
- B
- C
- D
Ta có $ MN//BC\Rightarrow \dfrac{AM}{MB}=\dfrac{AN}{NC}\Leftrightarrow \dfrac{10}{MB}=\dfrac{12}{6}\Rightarrow MB=5cm $
Xét tam giác vuông $ AMN $ có $ MN=\sqrt{A{{N}^{2}}-A{{M}^{2}}}=\sqrt{{{12}^{2}}-{{10}^{2}}}=\sqrt{44}=2\sqrt{11} $
Xét tam giác vuông $ ABC $ có $ BC=\sqrt{A{{C}^{2}}-A{{B}^{2}}}=\sqrt{{{18}^{2}}-{{15}^{2}}}=3\sqrt{11} $
$ \Rightarrow {{S}_{MNCB}}=\dfrac{\left( MN+BC \right)MB}{2}=\dfrac{\left( 2\sqrt{11}+3\sqrt{11} \right).5}{2}=25\sqrt{11}/2\left( c{{m}^{2}} \right) $
Câu 7: Cho hình vẽ , trong đó $ AB\text{//}CD $ và $ DE=EC $ . Trong các khẳng định sau, có bao nhiêu khẳng định đúng?

 $ \begin{array}{l} (I)\dfrac{AK}{EC}=\dfrac{KB}{DE}\,\,\,\, \\ \,\, \\ (II)AK=KB \\ \\ (III)\dfrac{AO}{AC}=\dfrac{AB}{DC}\,\,\, \\ \, \\ (IV)\dfrac{AK}{EC}=\dfrac{OB}{OD} \end{array} $
$ \begin{array}{l} (I)\dfrac{AK}{EC}=\dfrac{KB}{DE}\,\,\,\, \\ \,\, \\ (II)AK=KB \\ \\ (III)\dfrac{AO}{AC}=\dfrac{AB}{DC}\,\,\, \\ \, \\ (IV)\dfrac{AK}{EC}=\dfrac{OB}{OD} \end{array} $

- A
- B
- C
- D
Theo định lý Ta-lét:
Vì $ AK\text{//}EC $ nên $ \dfrac{AK}{EC}=\dfrac{OK}{OE} $ và $ BK\text{//}ED $ nên $ \dfrac{BK}{ED}=\dfrac{OK}{OE}=\dfrac{OB}{OD} $ từ đó $ \dfrac{AK}{EC}=\dfrac{KB}{DE} $ và $ \dfrac{AK}{EC}=\dfrac{OB}{OD} $
Mà $ EC=ED\Rightarrow AK=KB $ .
Nên (I), (II), (IV) đúng.
Vì $ AB\text{//}DC\Rightarrow \dfrac{AO}{OC}=\dfrac{AB}{DC} $ nên (III) sai.
Câu 8: Tỉ số của hai đoạn thẳng có độ dài $ AB=8cm $ và $ CD=22cm $ là
- A
- B
- C
- D
Ta có $ AB=8cm $ và $ CD=22cm $ $ \Rightarrow \dfrac{AB}{CD}=\dfrac{8}{22}=\dfrac{4}{11} $
Câu 9: Cho tam giác $ ABC $ , có $ MN//BC $ và độ dài các cạnh theo đơn vị (cm) như hình vẽ
 Khi đó chu vi tam giác ABC bằng
Khi đó chu vi tam giác ABC bằng
 Khi đó chu vi tam giác ABC bằng
Khi đó chu vi tam giác ABC bằng- A
- B
- C
- D
Ta có $ MN//BC\Rightarrow \dfrac{AM}{MB}=\dfrac{AN}{NC}\Leftrightarrow \dfrac{7}{MB}=\dfrac{8}{6}\Rightarrow MB=\dfrac{42}{8}=\dfrac{21}{4}cm $
Khi đó chu vi tam giác ABC bằng $ 9+6+8+7+\dfrac{21}{4}=\dfrac{141}{4}cm $
Câu 10: Cho tam giác $ ABC $ , đường trung tuyến $ AD $ , gọi $ K $ thuộc đoạn thẳng $ AD $ sao cho $ \dfrac{AK}{KD}=\dfrac{1}{2} $ . Gọi $ E $ là giao điểm của $ BK $ và $ AC $ . Tính tỉ số $ \dfrac{AE}{EC} $ .
- A
- B
- C
- D
Kẻ $ DM\text{//}BE\Rightarrow DM\text{//}KE $ , theo định lý Ta-lét trong tam giác $ ADM $ ta có $ \dfrac{AE}{EM}=\dfrac{AK}{KD}=\dfrac{1}{2} $
Xét tam giác $ BEC $ có $ DM\text{//}BE $ nên $ \dfrac{EM}{EC}=\dfrac{BD}{BC}=\dfrac{1}{2} $ (định lý Ta-lét)
Do đó $ \dfrac{AE}{EC}=\dfrac{AE}{EM}.\dfrac{EM}{EC}=\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4} $ .
Câu 11: Cho biết $ \dfrac{AB}{CD}=\dfrac{3}{5} $ và biết độ dài $ CD=20cm $ . Độ dài của $ AB $ bằng
- A
- B
- C
- D
Ta có $ \dfrac{AB}{CD}=\dfrac{3}{5} $ ; $ CD=20cm\Rightarrow \dfrac{AB}{20}=\dfrac{3}{5}\Rightarrow AB=\dfrac{20.3}{5}=12cm $
Câu 12: Cho tam giác $ ABC $ . Một đường thẳng song song với $ BC $ cắt các cạnh $ AB $ và $ AC $ theo thứ tự ở $ D $ và $ E $ . Chọn câu đúng.
- A
- B
- C
- D

Vì $ DE\text{//}BC $ nên theo định lý Ta-let ta có $ \dfrac{AD}{AB}=\dfrac{AE}{AC} $ .
Từ đó $ \dfrac{AD}{AB}+\dfrac{CE}{CA}=\dfrac{AE}{AC}+\dfrac{CE}{CA}=\dfrac{AC}{AC}=1 $ .
Câu 13: Giá trị $x$ theo hình vẽ là $ \left( MN//BC \right) $


- A
- B
- C
- D
Trong tam giác $ ABC $ , ta có:
$ \begin{array}{l} MN//BC\Rightarrow \dfrac{AM}{AB}=\dfrac{AN}{AC} \\ \Rightarrow \dfrac{3}{3+x}=\dfrac{2}{2+8}\Leftrightarrow \dfrac{3}{3+x}=\dfrac{1}{5} \\ \Leftrightarrow x+3=15\Rightarrow x=12 \end{array} $
Câu 14: Cho biết độ dài của $ AB $ gấp 6 lần độ dài của $ CD $ và độ dài của $ A'B' $ gấp 14 lần độ dài của $ CD $ . Tỉ số của hai đoạn thẳng $ AB $ và $ A'B' $ bằng
- A
- B
- C
- D
Độ dài $ AB $ gấp 6 lần độ dài của $ CD $ nên $ AB=6CD. $
Độ dài $ A'B' $ gấp 14 lần độ dài của $ CD $ nên $ A'B'=14CD. $
Tỉ số của hai đoạn thẳng $ AB $ và $ A'B' $ bằng $ \dfrac{AB}{A'B'}=\dfrac{6CD}{14CD}=\dfrac{3}{7} $
Câu 15: Hai đoạn thẳng $ AB=30cm,CD=12cm $ tỉ lệ với hai đoạn thẳng $ A'B'=40cm $ và $ C'D' $ . Đoạn thẳng $ C'D' $ có độ dài (theo đơn vị cm) là
- A
- B
- C
- D
Ta có $ \dfrac{AB}{A'B'}=\dfrac{CD}{C'D'}\Leftrightarrow \dfrac{30}{40}=\dfrac{12}{C'D'}\Rightarrow C'D'=\dfrac{12.40}{30}=16cm $
Câu 16: Cho hình thang $ ABCD(AB\text{//}CD) $ có diện tích $ 36c{{m}^{2}},AB=4cm,CD=8cm $ . Gọi $ O $ là giao điểm của hai đường chéo. Tính diện tích tam giác $ COD $ .
- A
- B
- C
- D

Kẻ $ AH\bot DC;OK\bot DC $ suy ra $ AH\text{//}OK $ .
Chiều cao của hình thang : $ AH=\dfrac{2{{S}_{ABCD}}}{AB+CD}=\dfrac{2.36}{4+8}=6(cm) $
Vì $ AB\text{//}DC $ (do $ ABCD $ là hình thang) nên theo định lý Ta-lét ta có
$ \dfrac{OC}{OA}=\dfrac{CD}{AB}=\dfrac{8}{4}=2\Rightarrow \dfrac{OC}{OC+OA}=\dfrac{2}{2+1}\Leftrightarrow \dfrac{OC}{AC}=\dfrac{2}{3} $
Vì $ AH\text{//}OK $ (cmt) nên theo định lý Ta-lét cho tam giác $ AHC $ ta có
$ \begin{array}{*{35}{l}} \dfrac{OK}{AH}=\dfrac{OC}{AC}=\dfrac{2}{3} \\ \Rightarrow OK=\dfrac{2}{3}AH\Leftrightarrow OK=\dfrac{2}{3}.6=4cm \end{array} $
Do đó $ {{S}_{COD}}=\dfrac{1}{2}OK.DC=\dfrac{1}{2}.4.8=16(c{{m}^{2}}) $ .
Câu 17: Giá trị x theo hình vẽ là $ \left( MN//BC \right) $


- A
- B
- C
- D
Trong tam giác $ ABC $ , ta có:
$ \begin{array}{l} MN//BC\Rightarrow \dfrac{AM}{AB}=\dfrac{AN}{AC} \\ \Rightarrow \dfrac{3}{3+6}=\dfrac{x}{x+4}\Leftrightarrow \dfrac{1}{3}=\dfrac{x}{x+4} \\ \Leftrightarrow x+4=3x\Rightarrow x=2 \end{array} $