Bài toán quỹ tích, cung chứa góc
Lý thuyết về Bài toán quỹ tích, cung chứa góc
*Định nghĩa:
* Cách giải bài toán quỹ tích:
Muốn chứng minh một quỹ tích (tập hợp) các điểm M thỏa mãn tính chất T là một hình H nào đó, ta phải chứng minh hai phần:
– Phần thuận: Mọi điểm có tính chất T đều thuộc hình H.
– Phần đảo: Mọi điểm M thuộc hình H đều có tính chất T.
Kết luận: Quỹ tích hay tập hợp các điểm M có tính chất T là hình H.
* Quỹ tích cung chứa góc:
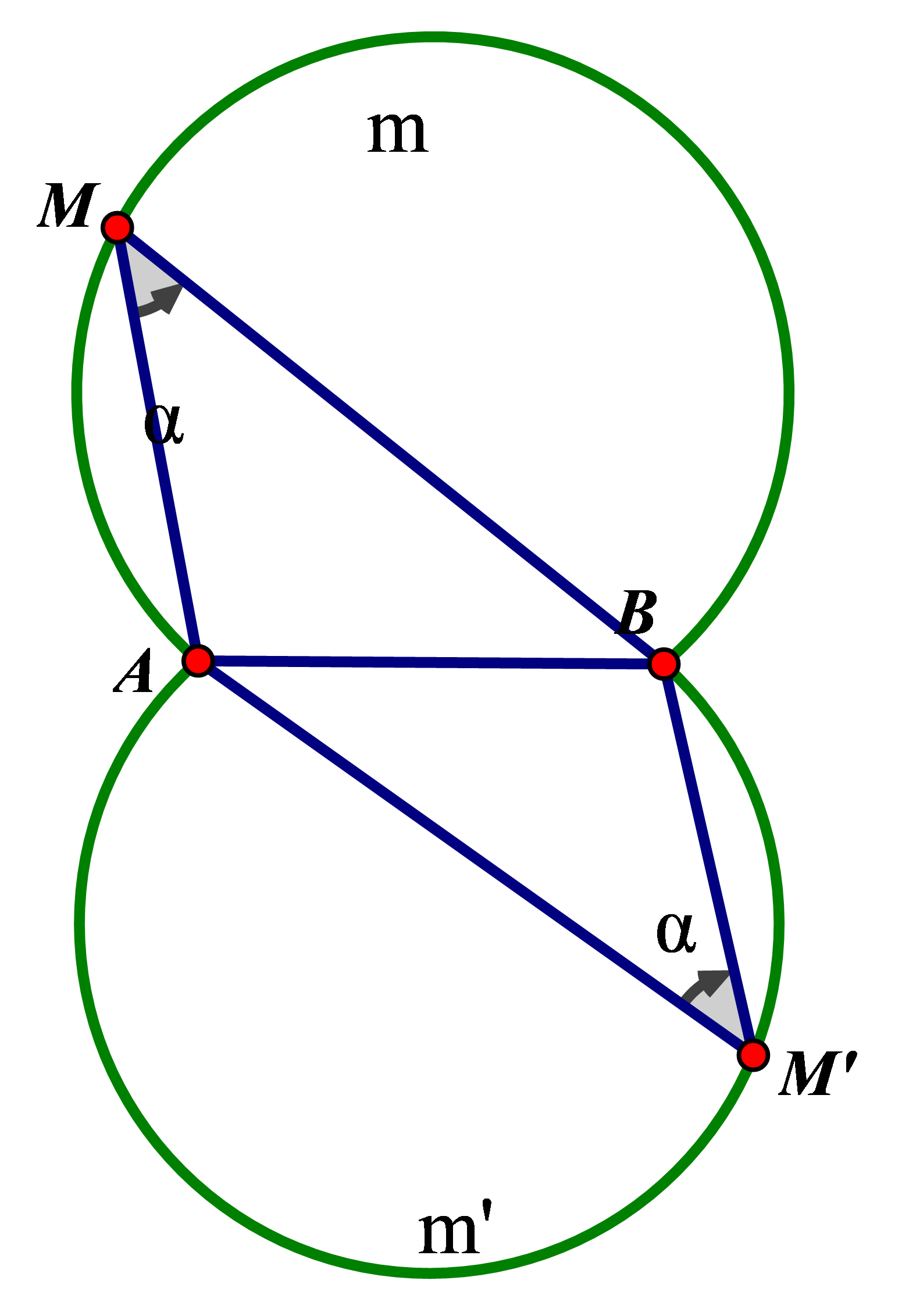
Quỹ tích(tập hợp): Các điểm $M$ tạo với hai nút của đoạn thẳng $AB$ cho trước một góc $\widehat {AMB}$ có số đo $α$ cho trước $\left( {{0^0} < \alpha < {{180}^0}} \right)$ là hai cung tròn có số đo là ${360^0} - 2\alpha $ đối xứng với nhau qua $AB$.
Bài tập tự luyện có đáp án
Câu 1: Cho đoạn thẳng $ AB $ cố định và hai điểm $ C,D $ bất kì thỏa mãn $ \widehat{ACB}=\widehat{ADB}={{120}^{0}} $ . Chọn kết luận đúng:
- A
- B
- C
- D


Có hai trường hợp xảy ra đó là: hai điểm $ C,D $ cùng thuộc một cung chứa góc hoặc thuộc hai cung chứa góc $ {{120}^{0}} $ dựng trên đoạn thẳng $ AB $
Câu 2: Quỹ tích các điểm $ M $ nhìn đoạn thẳng $ AB $ cho trước dưới một góc vuông là :
- A
- B
- C
- D
Quỹ tích các điểm $ M $ nhìn đoạn thẳng $ AB $ cho trước dưới một góc vuông là đường tròn đường kính $ AB $ (hai điểm $ A,B $ được coi là thuộc quỹ tích).
Câu 3: Đường tròn đường kính $ CD $ là quỹ tích của điểm nào dưới đây?
- A
- B
- C
- D
Quỹ tích các điểm $ M $ nhìn đoạn thẳng $ CD $ cho trước dưới một góc vuông là đường tròn đường kính $ CD $ .
Câu 4: Quỹ tích các điểm $ M $ nhìn đoạn thẳng $ AB $ cho trước dưới một góc vuông là
- A
- B
- C
- D
Quỹ tích các điểm $ M $ nhìn đoạn thẳng $ AB $ cho trước dưới một góc vuông là đường tròn đường kính $ AB $ .
Câu 5: Với đoạn thẳng $ AB $ và góc $ \alpha $ $ \left( 0{}^\circ < \alpha < 180{}^\circ \right) $ cho trước thì quỹ tích các điểm $ M $ thỏa mãn $ \widehat{AMB}=\alpha $ là :
- A
- B
- C
- D
Với đoạn thẳng $ AB $ và góc $ \alpha $ $ \left( 0{}^\circ < \alpha < 180{}^\circ \right) $ cho trước thì quỹ tích các điểm $ M $ thỏa mãn $ \widehat{AMB}=\alpha $ là hai cung chứa góc $ \alpha $ dựng trên đoạn $ AB $ .
Hai cung chứa góc $ \alpha $ nói trên là hai cung tròn đối xứng nhau qua $ AB $ . Hai điểm $ A,B $ được coi là thuộc quỹ tích.
Câu 6: Cho hình vẽ sau, chọn kết luận đúng:


- A
- B
- C
- D
Quan sát hình vẽ ta thấy các điểm $ B,D $ thuộc cung chứa góc $ {{80}^{0}} $ dựng trên đoạn $ AC $ , còn điểm $ E $ thuộc cung chứa góc $ {{75}^{0}} $ dựng trên đoạn $ AC $ .
Do đó chỉ có đáp án hai điểm $ B,D $ cùng thuộc cung chứa góc $ {{80}^{0}} $ dựng trên đoạn $ AC $ là đúng.