Dấu hiệu nhận biết tiếp tuyến của đường tròn
Lý thuyết về Dấu hiệu nhận biết tiếp tuyến của đường tròn
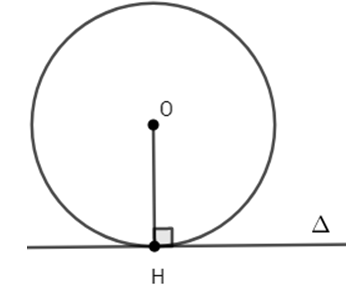
* Định nghĩa tiếp tuyến của đường tròn:
- Đường thẳng được gọi là tiếp tuyến của đường tròn nếu nó có một điểm chung với đường tròn. Điểm đó được gọi là tiếp điểm
Ví dụ: Δ là tiếp tuyến của đường tròn (O), H gọi là tiếp điểm
*Tính chất:
-Tiếp tuyến của đường tròn vuông góc với bán kính tại tiếp điểm.
*Dấu hiệu nhận biết:
- Nếu một đường thẳng đi qua 1 điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn
Bài tập tự luyện có đáp án
Câu 1: Cho đường tròn (O) , dây AB khác đường kính. Qua O kẻ đường vuông góc với AB , cắt tiếp tuyến tại A của đường tròn ở điểm C. Chọn khẳng định đúng?
- A
- B
- C
- D

Gọi OC cắt AB tại I . Vì OA=OB ⇒ΔAOB cân ở O. Mà OI⊥AB ⇒ OI là phân giác góc ^AOB .
⇒ΔAOC=ΔBOC(c.g.c) ⇒^OBC=^OAC=90o . Suy ra BC là tiếp tuyến của (O)
Câu 2: Từ một điểm A ở bên ngoài đường tròn (O;R) , vẽ hai tiếp tuyến AB, AC với (O) . Đường thẳng vuông góc với OB tại O cắt tia AC tại N. Đường thẳng vuông góc với OC cắt tia AB tại M. Tứ giác AMON là hình gì?
- A
- B
- C
- D

Dễ có AMON là hình bình hành (vì ON//AM;OM//AN ).
Ta chứng minh OM=ON .
Xét tam giác OBM và tam giác OCN có :
^OBM=^OCN=90o; OB=OC=R, và ^OMB=^ONC=ˆA
⇒ΔOBM=ΔON⇒AMON là hình thoi.
Câu 3: Cho (O;5cm) . Đường thẳng d là tiếp tuyến của đường tròn (O;5cm) . Khi đó
- A
- B
- C
- D
Khoảng cách từ tâm của một đường tròn đến tiếp tuyến bằng bán kính của đường tròn đó.
Câu 4: Cho đường tròn (O;R) đường kính AB . Vẽ dây AC sao cho ^ABC=300 . Trên tia đối cỉa tia AB lấy điểm M sao cho AM=R . Tính độ dài MC theo R .
- A
- B
- C
- D

Áp dụng định lý Pytago cho tam giác vuông OCM , ta có OM2=OC2+MC2
⇒MC2=OM2−OC2=3R2⇒MC=√3R
Câu 5: Cho (O;R) . Đường thẳng d là tiếp tuyến của đường tròn (O;R) tại tiếp điểm A khi
- A
- B
- C
- D
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Câu 6: Cho tam giác ABC có AC=3cm,AB=4cm,BC=5cm . Vẽ đường tròn (C;CA) . Khẳng định nào sau đây đúng?
- A
- B
- C
- D

Xét tam giác ABC có:
BC2=52=25;AB2+AC2=42+32=25;⇒BC2=AB2+AC2
⇒ΔABC vuông tại A (định lý Pytago đảo)
⇒AB⊥AC mà A∈(C;CA) nên AB là tiếp tuyến của (C;CA)