Hình cầu. Diện tích hình cầu và thể tích hình cầu
Lý thuyết về Hình cầu. Diện tích hình cầu và thể tích hình cầu
1. Khái niệm hình cầu
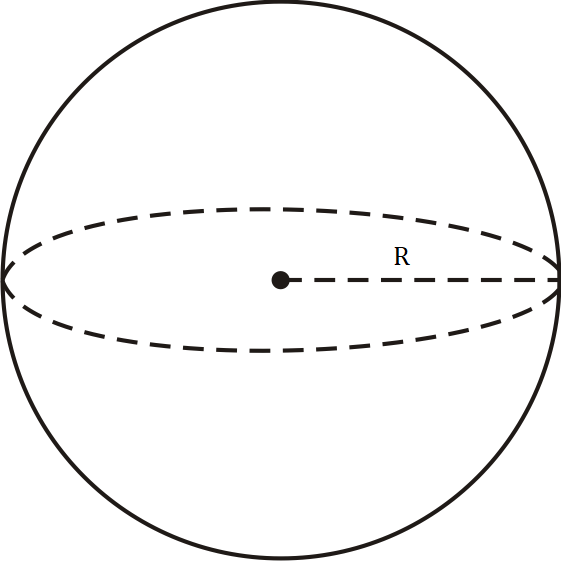
Khi quay nửa hình tròn tâp $O$, bán kính $R$ một vòng quanh đường kính $AB$ cố định thì được một hình cầu.
– Điểm $O$ được gọi là tâm, độ dài $R$ là bán kính của hình cầu.
– Nửa đường tròn trong phép quay nói trên tạo nên mặt cầu
2. Diện tích mặt cầu
Công thức diện tích mặt cầu: \[S = 4\pi {r^2} = \pi {d^2}\]
R là bán kính, d là đường kính mặt cầu.
3. Thể tích hình cầu
Thể tích hình cầu bán kính $R$ : \[V = \dfrac{4}{3}\pi {r^3}\]
Bài tập tự luyện có đáp án
Câu 1: Cho mặt cầu có thể tích $ V=288\pi (c{{m}^{3}}) $ . Tính đường kính mặt cầu.
- A
- B
- C
- D
Ta có $ V=\dfrac{4}{3}\pi {{R}^{3}}=288\pi \Rightarrow {{R}^{3}}=216\Rightarrow R=6cm $
Từ đó đường kính mặt cầu là $ d=2R=2.6=12cm $ .
Câu 2: Diện tích mặt cầu đường kính $ d $ là:
- A
- B
- C
- D
Diện tích mặt cầu đường kính $ d $ là $ S=\pi {{d}^{2}} $
Câu 3: Khi cắt mặt cầu bán kính $ R $ bởi một mặt phẳng ta được:
- A
- B
- C
- D
Khi cắt mặt cầu bán kính $ R $ bởi một mặt phẳng ta được đường tròn bán kính nhỏ hơn hoặc bằng $ R $ .
Câu 4: Đường kính hình cầu có thể tích $ V $ là:
- A
- B
- C
- D
Ta có: $ V=\dfrac{4}{3}\pi {{R}^{3}}\Leftrightarrow {{R}^{3}}=\dfrac{3V}{4\pi }\Leftrightarrow R=\sqrt[3]{\dfrac{3V}{4\pi }}\Leftrightarrow d=2R=2.\sqrt[3]{\dfrac{3V}{4\pi }}=\sqrt[3]{\dfrac{{{2}^{3}}.3V}{4\pi }}=\sqrt[3]{\dfrac{6V}{\pi }} $
Câu 5: Cắt mặt cầu tâm $ O $ bán kính $ R=6cm $ bởi một mặt phẳng đi qua tâm ta được đường tròn có chu vi:
- A
- B
- C
- D
Chu vi đường tròn lớn là: $ C=2\pi R=2\pi .6=12\pi \left( cm \right) $
Câu 6: Khi quay nửa hình tròn quanh một đường kính cố định ta được:
- A
- B
- C
- D
Khi quay nửa hình tròn quanh một đường kính cố định ta được một hình cầu.
Câu 7: Cho mặt cầu có thể tích $ V=972\pi (c{{m}^{3}}) $ . Tính đường kính mặt cầu.
- A
- B
- C
- D
Ta có $ V=\dfrac{4}{3}\pi {{R}^{3}}=972\pi \Rightarrow {{R}^{3}}=729\Rightarrow R=9cm $
Từ đó đường kính mặt cầu là $ d=2R=2.9=18cm $ .
Câu 8: Cho hình cầu có đường kính $ d=6cm $ . Diện tích mặt cầu là.
- A
- B
- C
- D
Vì đường kính $ d=6cm $ nên bán kính hình cầu $ R=\dfrac{6}{2}=3cm $
Diện tích mặt cầu $ S=4\pi {{R}^{2}}=4\pi {{.3}^{2}}=36\pi (c{{m}^{2}}) $ .