Một số hệ thức về cạnh và đường cao trong tam giác vuông
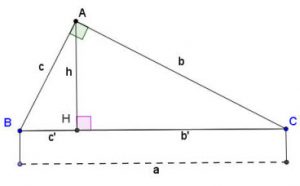
Lý thuyết về Một số hệ thức về cạnh và đường cao trong tam giác vuông
- Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền: $b^2 = a \cdot b'; c^2 = a \cdot c'$.
- Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền: $h2 = b'c'$.
- Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng: $b \cdot c = a \cdot h$.
- Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông: $\dfrac{1}{h^2} = \dfrac{1}{b^2} + \dfrac{1}{c^2}$.
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ . Biết $ AB:AC=3:4 $ và $ AB+AC=21cm $ . Độ dài các đoạn $ AH,BH,CH $ lần lượt là
- A
- B
- C
- D
Ta có $ AB=9;AC=12;BC=15 $
$ \Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12.9}{15}=7,2 $
$ A{{B}^{2}}=BH.BC\Rightarrow BH=\dfrac{A{{B}^{2}}}{BC}=\dfrac{81}{15}=5,4 $
$ \Rightarrow CH=BC-BH=15-5,4=9,6 $
Vậy $ AH=7,2;BH=5,4;CH=9,6 $ .
Câu 2: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ . Gọi $ D $ và $ E $ lần lượt là hình chiếu vuông góc của $ H $ trên $ AB,AC $ (hình vẽ) 
Tỉ số $ \dfrac{A{{B}^{3}}}{A{{C}^{3}}} $ bằng
Tỉ số $ \dfrac{A{{B}^{3}}}{A{{C}^{3}}} $ bằng
- A
- B
- C
- D
Tam giác vuông $ AHB $ có $ B{{H}^{2}}=BD.AB\Rightarrow BD=\dfrac{B{{H}^{2}}}{AB} $
Tam giác vuông $ AHC $ có $ H{{C}^{2}}=AC.EC\Rightarrow EC=\dfrac{H{{C}^{2}}}{AC} $
Từ đó $ \dfrac{BD}{EC}=\dfrac{H{{B}^{2}}}{AB}:\dfrac{H{{C}^{2}}}{A{{C}^{2}}}=\dfrac{H{{B}^{2}}}{H{{C}^{2}}}.\dfrac{AC}{AB} $
mà dễ dàng ta có $ \dfrac{A{{B}^{2}}}{A{{C}^{2}}}=\dfrac{HB}{HC} $ nên $ \dfrac{BD}{EC}=\dfrac{A{{B}^{4}}}{A{{C}^{4}}}.\dfrac{AC}{AB}\Leftrightarrow \dfrac{BD}{EC}=\dfrac{A{{B}^{3}}}{A{{C}^{3}}} $ .
Câu 3: Tìm $ x,y $ trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
$ A{{B}^{2}}=BH.BC\Leftrightarrow BH=\dfrac{A{{B}^{2}}}{BC}=\dfrac{144}{20}=7,2\Rightarrow CH=BC-BH=20-7,2=12,8 $ .
Vậy $ x=7,2;y=12,8 $ .
Câu 4: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ . Cho biết $ BH=9cm,CH=16cm $ . Gọi $ D,E $ lần lượt là hình chiếu vuông góc của $ H $ trên các cạnh $ AB $ và $ AC $ . Các đường thẳng vuông góc với $ DE $ tại $ D $ và $ E $ lần lượt cắt $ BC $ tại $ M,N $ . (hình vẽ) 
Diện tích tứ giác $ DENM $ bằng
Diện tích tứ giác $ DENM $ bằng
- A
- B
- C
- D
Vì $ DM\bot DE,EN\bot DE\Rightarrow DM\parallel EN;\widehat{D}=\widehat{E}=90{}^\circ $ nên $ DENM $ là hình thang vuông
Ta có $ DM=\dfrac{BH}{2}=4,5;EN=\dfrac{CH}{2}=8;DE=12 $
Nên $ {{S}_{DENM}}=\dfrac{(DM+DN).DE}{2}=\dfrac{(4,5+8).12}{2}=75\,c{{m}^{2}} $ .
Câu 5: Tính $ x $ trong hình vẽ sau


- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
$ \dfrac{1}{M{{D}^{2}}}=\dfrac{1}{M{{N}^{2}}}+\dfrac{1}{M{{P}^{2}}}\Rightarrow \dfrac{1}{64}=\dfrac{1}{{{x}^{2}}}+\dfrac{1}{{{x}^{2}}}\Rightarrow \dfrac{1}{64}=\dfrac{2}{{{x}^{2}}}\Rightarrow {{x}^{2}}=128\Leftrightarrow x=8\sqrt{2} $ .
Vậy $ x=8\sqrt{2} $ .
Câu 6: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ . Biết $ AB:AC=5:12 $ và $ AB+AC=34cm $ . Tính các cạnh của tam giác $ ABC $ .
- A
- B
- C
- D
Theo giả thiết: $ AB:AC=5:12 $ .
Suy ra $ \dfrac{AB}{5}=\dfrac{AC}{12}=\dfrac{AB+AC}{5+12}=\dfrac{34}{17}=2 $ . Do đó $ AB=5.2=10\,(cm);AC=2.12=24\,(cm) $ .
Tam giác $ ABC $ vuông tại $ A $ , theo định lý Pytago ta có $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}={{10}^{2}}+{{24}^{2}}=676 $ , suy ra $ BC=26\,cm $ .
Câu 7: Trong một tam giác vuông, nghịch đảo bình phương đường cao ứng với cạnh huyền bằng
- A
- B
- C
- D
Trong một tam giác vuông, nghịch đảo bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo bình phương hai cạnh góc vuông.
Câu 8: Trong hình bên, độ dài BH bằng:


- A
- B
- C
- D
Ta có: Theo định lý Pytago trong tam giác ABC ta có
$ \begin{array}{l}
& B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}} \\
& ={{3}^{2}}+{{4}^{2}} \\
& =25 \\
& BC=\sqrt{25}=5cm \\
\end{array} $ .
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ABC đường cao AH ta có:
$ \begin{array}{l}
& A{{B}^{2}}=BC.BH \\
& \Rightarrow BH=\dfrac{A{{B}^{2}}}{BC} \\
& =\dfrac{{{3}^{2}}}{5}=1,8 \\
\end{array} $
Câu 9: Tính $ x $ trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
$ \dfrac{1}{A{{H}^{2}}}=\dfrac{1}{A{{B}^{2}}}+\dfrac{1}{A{{C}^{2}}}\Rightarrow AH=\dfrac{AB.AC}{\sqrt{A{{B}^{2}}+A{{C}^{2}}}}=\dfrac{15.20}{\sqrt{{{15}^{2}}+{{20}^{2}}}}=12 $ .
Vậy $ x=12 $ .
Câu 10: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ . Gọi $ D $ và $ E $ lần lượt là hình chiếu vuông góc của $ H $ trên $ AB,AC $ (hình vẽ) 
Tỉ số $ \dfrac{A{{B}^{2}}}{A{{C}^{2}}} $ bằng
Tỉ số $ \dfrac{A{{B}^{2}}}{A{{C}^{2}}} $ bằng
- A
- B
- C
- D
Xét tam giác vuông $ ABC $ có $ AH $ là đường cao nên $ A{{B}^{2}}=BH.BC;A{{C}^{2}}=CH.BC $
Nên $ \dfrac{A{{B}^{2}}}{A{{C}^{2}}}=\dfrac{BH.BC}{CH.BC}=\dfrac{HB}{HC} $
Câu 11: Tính $ x,y $ trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
$ A{{H}^{2}}=BH.CH\Rightarrow A{{H}^{2}}=2.5\Rightarrow AH=\sqrt{10} $ .
Áp dụng định lý Pytago cho tam giác vuông $ AHB;AHC $ ta có
$ AB=\sqrt{A{{H}^{2}}+H{{B}^{2}}}=\sqrt{10+4}=\sqrt{14}\,;\,\,AC=\sqrt{A{{H}^{2}}+H{{C}^{2}}}=\sqrt{10+25}=\sqrt{35} $
Vậy $ x=\sqrt{14};y=\sqrt{35} $ .
Câu 12: Tính $ x,y $ trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
$ A{{B}^{2}}=BH.BC\Leftrightarrow BH=\dfrac{A{{B}^{2}}}{BC}=\dfrac{100}{16}=6,25\Rightarrow CH=BC-BH=16-6,25=9,75 $ .
Vậy $ x=6,25;y=9,75 $ .
Câu 13: Cho tam giác $ CDE $ nhọn, đường cao $ CH $ . Gọi $ M,N $ theo thứ tự là hình chiếu của $ H $ lên $ CD,DE $ . (hình vẽ) 
Tam giác $ CMN $ đồng dạng với tam giác nào dưới đây?
Tam giác $ CMN $ đồng dạng với tam giác nào dưới đây?
- A
- B
- C
- D
Câu trước ta có $ CM.CD=CN.CE\Leftrightarrow \dfrac{CM}{CN}=\dfrac{CE}{CD} $
Xét $ \Delta CMN $ và $ \Delta CED $ có $ \widehat{C} $ chung và $ \dfrac{CM}{CN}=\dfrac{CE}{CD} $ nên $ \Delta CMN\sim \Delta CED $ (c – g – c)
Câu 14: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ . Biết $ AB:AC=3:4 $ và $ AB+AC=21cm $ . Độ dài các cạnh của tam giác $ ABC $ lần lượt là
- A
- B
- C
- D
Theo giả thiết: $ AB:AC=3:4 $
Suy ra $ \dfrac{AB}{3}=\dfrac{AC}{4}=\dfrac{AB+AC}{3+4}=3 $ . Do đó $ AB=3.3=9\,(cm);AC=3.4=12\,(cm) $ .
Tam giác $ ABC $ vuông tại $ A $ , theo định lý Pytago ta có $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}={{9}^{2}}+{{12}^{2}}=225 $ , suy ra $ BC=15\,cm $ .
Câu 15: Cho hình vẽ bên, tam giác $ ABC $ vuông tại $ A $ ,cạnh $ AB=10cm $ ,đường cao $ AH=8cm $ . Độ dài cạnh $ BC $ bằng:


- A
- B
- C
- D
Theo pitago, tam giác vuông $ AHB $ $ \Rightarrow BH=6cm $
Theo hệ thức lượng trongtam giác có: $ A{{H}^{2}}=BH.HC\Rightarrow HC=\dfrac{32}{3}\Rightarrow BC=\dfrac{50}{3}cm $ .
Câu 16: Trên hình 1.2 ta có:


- A
- B
- C
- D
Áp dụng hệ thức $ {{b}^{2}}=b'.a $ ta có $ {{9}^{2}}=x.15 $ suy ra $ x=5,4 $ và $ y=15-5,4=9,6 $ .
Câu 17: Cho tam giác $ CDE $ nhọn, đường cao $ CH $ . Gọi $ M,N $ theo thứ tự là hình chiếu của $ H $ lên $ CD,DE $ . (hình vẽ) 
Tích $ CD.CM $ bằng
Tích $ CD.CM $ bằng
- A
- B
- C
- D
Tam giác $ CHD $ vuông tại $ H $ , ta có $ C{{H}^{2}}=CM.CD $
Tam giác $ CHE $ vuông tại $ H $ , ta có $ C{{H}^{2}}=CN.CE $
Nên $ CM.CD=CN.CE $
Câu 18: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ . Cho biết $ BH=9cm,CH=16cm $ . Gọi $ D,E $ lần lượt là hình chiếu vuông góc của $ H $ trên các cạnh $ AB $ và $ AC $ . Các đường thẳng vuông góc với $ DE $ tại $ D $ và $ E $ lần lượt cắt $ BC $ tại $ M,N $ . (hình vẽ) 
Độ dài đoạn thẳng $ DE $ bằng
Độ dài đoạn thẳng $ DE $ bằng
- A
- B
- C
- D
Tứ giác $ AEHD $ là hình chữ nhật vì $ \widehat{A}=\widehat{E}=\widehat{D}=90{}^\circ $ nên $ DE=AH $
Xét $ \Delta ABC $ vuông tại $ A $ có $ A{{H}^{2}}=HB.HC=16.9=144\Rightarrow AH=12 $
Nên $ DE=12\,cm $ .
Câu 19: Tìm $ x,y $ trong hình vẽ sau


- A
- B
- C
- D
Theo định lý Pytago ta có $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}\Leftrightarrow B{{C}^{2}}=100\Leftrightarrow BC=10 $ .
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có $ A{{B}^{2}}=BH.BC\Rightarrow BH=\dfrac{A{{B}^{2}}}{BC}=\dfrac{{{6}^{2}}}{10}=3,6 $ hay $ x=3,6\Rightarrow CH=BC-BH=10-3,6=6,4 $ hay $ y=6,4 $ .
Vậy $ x=3,6;y=6,4 $ .
Câu 20: Tìm $ x,y $ trong hình vẽ sau 
- A
- B
- C
- D
Theo định lý Pytago ta có $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}\Leftrightarrow B{{C}^{2}}=74\Leftrightarrow BC=\sqrt{74} $ .
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có $ AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{5.7}{\sqrt{74}}=\dfrac{35\sqrt{74}}{74} $ .
Vậy $ x=\dfrac{35\sqrt{74}}{74};y=\sqrt{74} $ .
Câu 21: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ . Cho biết $ BH=4cm,CH=9cm $ . Gọi $ D,E $ lần lượt là hình chiếu vuông góc của $ H $ trên các cạnh $ AB $ và $ AC $ . Các đường thẳng vuông góc với $ DE $ tại $ D $ và $ E $ lần lượt cắt $ BC $ tại $ M,N $ . (hình vẽ) 
Diện tích tứ giác $ DENM $ bằng
Diện tích tứ giác $ DENM $ bằng
- A
- B
- C
- D
Vì $ DM\bot DE,EN\bot DE\Rightarrow DM\parallel EN;\widehat{D}=\widehat{E}=90{}^\circ $ nên $ DENM $ là hình thang vuông
Ta có $ DM=\dfrac{BH}{2}=2;EN=\dfrac{CH}{2}=4,5;DE=6 $
Nên $ {{S}_{DENM}}=\dfrac{(DM+DN).DE}{2}=19,5\,c{{m}^{2}} $ .
Câu 22: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ . Cho biết $ BH=9\,cm,CH=16\,cm $ . Gọi $ D,E $ lần lượt là hình chiếu vuông góc của $ H $ trên các cạnh $ AB $ và $ AC $ . Các đường thẳng vuông góc với $ DE $ tại $ D $ và $ E $ lần lượt cắt $ BC $ tại $ M,N $ . (hình vẽ) 
Độ dài đoạn thẳng $ DE $ bằng
Độ dài đoạn thẳng $ DE $ bằng
- A
- B
- C
- D
Tứ giác $ AEHD $ là hình chữ nhật vì $ \widehat{A}=\widehat{E}=\widehat{D}=90{}^\circ $ nên $ DE=AH $
Xét $ \Delta ABC $ vuông tại $ A $ có $ A{{H}^{2}}=HB.HC=9.16=144\Rightarrow AH=12 $
Nên $ DE=12cm $ .
Câu 23: Tính $ x $ trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
$ \dfrac{1}{M{{D}^{2}}}=\dfrac{1}{M{{N}^{2}}}+\dfrac{1}{M{{P}^{2}}}\Rightarrow \dfrac{1}{64}=\dfrac{1}{{{x}^{2}}}+\dfrac{1}{{{x}^{2}}}\Leftrightarrow \dfrac{1}{64}=\dfrac{2}{{{x}^{2}}}\Rightarrow {{x}^{2}}=128\Leftrightarrow x=8\sqrt{2} $ .
Vậy $ x=8\sqrt{2} $ .
Câu 24: Tính $ x $ trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai) 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông $ ABC $ ta có
$ \dfrac{1}{A{{H}^{2}}}=\dfrac{1}{A{{B}^{2}}}+\dfrac{1}{A{{C}^{2}}}\Leftrightarrow \dfrac{1}{A{{H}^{2}}}=\dfrac{A{{B}^{2}}+A{{C}^{2}}}{A{{B}^{2}}.A{{C}^{2}}}\Leftrightarrow A{{H}^{2}}=\dfrac{A{{B}^{2}}.A{{C}^{2}}}{A{{B}^{2}}+A{{C}^{2}}} $
$ \Rightarrow AH=\dfrac{AB.AC}{\sqrt{A{{B}^{2}}+A{{C}^{2}}}}=\dfrac{15.20}{\sqrt{{{15}^{2}}+{{20}^{2}}}}=12 $ .
Vậy $ x=12$ .
Câu 25: Cho tam giác $ ABC $ vuông tại $ A $ , đường cao $ AH $ . Biết $ AB:AC=5:12 $ và $ AB+AC=34cm $ . Tính độ dài các đoạn $ AH,BH,CH $ (làm tròn đến chữ số thập phân thứ hai)
- A
- B
- C
- D
Dễ dàng ta có $ AB=10;AC=24;BC=26 $ .
$ \Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{10.24}{26}\approx 9,23 $ ;
$ A{{B}^{2}}=BH.BC\Rightarrow BH=\dfrac{A{{B}^{2}}}{BC}=\dfrac{{{10}^{2}}}{13}=\dfrac{100}{13}\approx 7,69 $ .
$ \Rightarrow CH=BC-BH=26-7,69=18,31 $ .
Vậy $ AH\approx 9,23;BH\approx 7,69;CH\approx 18,31 $ .
Câu 26: Cho tam giác $ABC$ vuông tại $C$. Trong các hệ thức dưới đây hệ thức nào đúng ?
- A
- B
- C
- D
Câu 27: Tính $ x,y $ trong hình vẽ sau 
- A
- B
- C
- D
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
$ A{{H}^{2}}=BH.CH\Rightarrow A{{H}^{2}}=1.4\Rightarrow AH=2 $ .
Áp dụng định lý Pytago cho tam giác vuông $ AHB;AHC $ ta có
$ AB=\sqrt{A{{H}^{2}}+H{{B}^{2}}};AC=\sqrt{A{{H}^{2}}+H{{C}^{2}}}=2\sqrt{5} $ .
Vậy $ x=\sqrt{5};y=2\sqrt{5} $ .
Câu 28: Cho tam giác $ ABC $ vuông tại $ A $ , chiều cao $ AH $ và $ AB=5;AC=12 $ . Đặt $ BC=y;AH=x $ . Giá trị của $ x,y $ lần lượt là
- A
- B
- C
- D
Theo định lý Pytago ta có $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}\Leftrightarrow B{{C}^{2}}=169\Leftrightarrow BC=13 $ .
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
$ AH.BC=AB.AC\Leftrightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{5.12}{13}=\dfrac{60}{13} $ .
Vậy $ x=\dfrac{60}{13};y=13 $ .
Câu 29: Tính $ x,y $ trong hình vẽ sau 
- A
- B
- C
- D
Theo định lý Pytago ta có \[ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}\Leftrightarrow B{{C}^{2}}=25\Leftrightarrow BC=5 \] .
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có
\[ A{{B}^{2}}=BH.BC\Rightarrow BH=\dfrac{A{{B}^{2}}}{BC}=\dfrac{{{3}^{2}}}{5}=1,8 \] hay \[ x=1,8 \] .
\[ \Rightarrow CH=BC-BH=5-1,8=3,2 \] hay \[ y=3,2 \] .
Vậy \[ x=1,8;y=3,2 \] .