Trường hợp cạnh – cạnh – cạnh (c.c.c)
Lý thuyết về Trường hợp cạnh – cạnh – cạnh (c.c.c)
1. Trường hợp cạnh – cạnh – cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
ΔABC và ΔA′B′C′ có:
AB=A′B′
BC=B′C′
AC=A′C′
⇒ΔABC=ΔA′B′C′
Bài tập tự luyện có đáp án
Câu 1: Cho hình vẽ bên 
Khẳng định nào sai?
Khẳng định nào sai?
- A
- B
- C
- D
Xét ΔDBC có DB=DC⇒^DCB=^DBC
Dễ dàng chứng minh được ΔDBA=ΔDCA(c.c.c)⇒{^ABD=^ACD^BDA=^CDA
Câu 2: Cho hình vẽ sau: /07.png)
Khẳng định nào sau đây không đúng ?
/07.png)
Khẳng định nào sau đây không đúng ?
- A
- B
- C
- D
Xét tam giác AEB và tam giác AEC có:
Cạnh chung AE;
AB = AC (giả thiết);
EB = EC (giả thiết)
⇒ΔAEB=ΔAEC(c.c.c)
⇒^BAE=^CAE;^AEB=^AEC;^ABE=^ACE
Ta có: ^BAE=^CAE và tia AE nằm giữa hai tia AB, AB.
⇒ Tia AE là tia phân giác của ^BAC .
Câu 3: Cho hình vẽ sau: /04.png)
Cho biết ^AMB=110o . Khi đó số đo ^AMN là:
/04.png)
Cho biết ^AMB=110o . Khi đó số đo ^AMN là:
- A
- B
- C
- D
Xét tam giác AMN và tam giác BMN có:
Cạnh chung MN;
AM = BM (giả thiết);
AN = BN (giả thiết)
⇒ΔAMN=ΔBMN(c.c.c)
⇒^AMN=^BMN .
Vì tia MN nằm giữa hai tia MA và MB nên ^AMB=^AMN+^BMN=2^AMN
⇒^AMN=12^AMB=12.110o=55o .
Câu 4: Chọn câu trả lời đúng
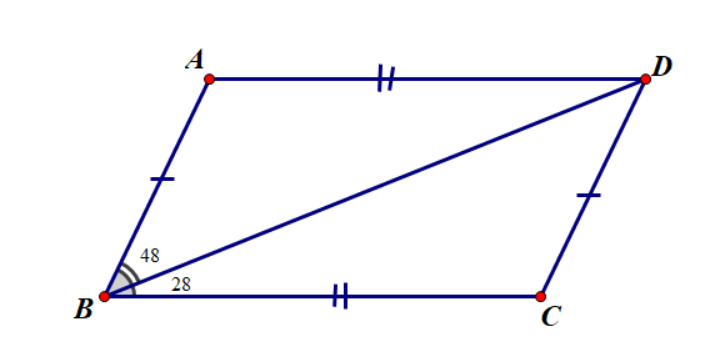
Cho hình vẽ bên, có AD=BC;AB=CD
 Số đo góc ^ADB bằng
Số đo góc ^ADB bằng
 Số đo góc ^ADB bằng
Số đo góc ^ADB bằng- A
- B
- C
- D
Xét ΔABD và ΔCDB có {BDchungAB=CDAD=BC⇒ΔABD=ΔCDB(c.c.c)⇒^ADB=^CBD=28o
Câu 5: Cho hình vẽ 
Hãy chọn câu trả lời đúng.
Hãy chọn câu trả lời đúng.
- A
- B
- C
- D
Xét ΔBAD và ΔEAC có {BD=ECAC=ABAD=AE⇒ΔBAD=ΔEAC(c.c.c)⇒^BAD=^EAC
Câu 6: Cho tam giác ABC có AB = AC. Trên cạnh BC lấy các điểm D và E sao cho BD=EC .
Khẳng định nào đúng trong các khẳng định sau:
- A
- B
- C
- D
/09.png)
Xét tam giác ABD và tam giác ACE có:
AB = AC (giả thiết);
AD = AE (giả thiết);
BD = DE (giả thiết)
⇒ΔABD=ΔACE (c.c.c)
⇒^ADB=^AEC (1); ^ABD=^ACE;^BAD=^CAE
Ta có: ^ADB+^ADE=180o (kề bù). (2)
^AED+^AEC=180o (kề bù). (3)
Từ (1) (2) và (3) suy ra ^ADE=^AED .
Câu 7: Cho hình vẽ sau: /06.png)
Số đo góc ^PEN là:
/06.png)
Số đo góc ^PEN là:
- A
- B
- C
- D
Xét tam giác MPE và tam giác NPE có:
Cạnh chung PE;
MP = PN; EM = EN (giả thiết)
⇒ΔMPE=ΔNPE(c.c.c)⇒^MEP=^NEP
Xét tam giác MPE có: ^MPE+^PME+^MEP=180o
⇒^MEP=180o−^MPE−^PME=180o−58o−90o=32o .
Vậy ^NEP=^MEP=32o .
Câu 8: Chọn câu trả lời đúng. Cho tam giác ABC có AB=AC . Gọi M là trung điểm của BC thì
Cho tam giác ABC có AB=AC . Gọi M là trung điểm của BC thì
- A
- B
- C
- D
tam giác ABC có AB=AC⇒ΔABC cân tại A mà M là trung điểm của BC nên AM là tia phân giác góc BAC .
Câu 9: Cho hình vẽ sau 
Khẳng định sai là
Khẳng định sai là
- A
- B
- C
- D
Ta có ΔABC:AB=AC⇒D là trung điểm của BC nên AD⊥BC ; AD là phân giác góc ^BAC
Chưa đủ dữ kiện để kết luận AB//CE .
Câu 10: Chọn câu trả lời đúng. Tính số đo góc ACD ở hình bên

Tính số đo góc ACD ở hình bên
- A
- B
- C
- D
Xét ΔABC và ΔADC có {ACchungAB=ADBC=DC⇒ΔABC=ΔADC(c.c.c)⇒^ACB=^ACD=110o
Câu 11: Cho đoạn thẳng AB. Lấy hai điểm C và D nằm ngoài đoạn AB và thuộc hai nửa mặt phẳng đối nhau có bờ là AB sao cho CA = CB, DA = DB. Chọn khẳng định đúng trong các khẳng định sau:
- A
- B
- C
- D
/03.png)
Xét tam giác ACD và tam giác BCD có:
Cạnh AB chung;
AC = BC (giả thiết);
AD = DB (giả thiết)
⇒ΔACD=ΔBCD(c.c.c)
⇒^ACD=^BCD;^ADC=^BDC .
Câu 12: Cho MB=MC;AM=MD;AB=CD . Hai tam giác nào dưới đây bằng nhau ?
- A
- B
- C
- D
Ta có {MB=MCAM=MDAB=CD⇒ΔBMA=ΔCMD
Câu 13: Cho hình vẽ sau:
/05.png) Khẳng định nào sau đây không đúng?
Khẳng định nào sau đây không đúng?
/05.png) Khẳng định nào sau đây không đúng?
Khẳng định nào sau đây không đúng?
- A
- B
- C
- D
Xét tam giác ABD và tam giác CDB có:
Cạnh chung BD;
AB = CD (giả thiết);
AD = BC (giả thiết)
⇒ΔABD=ΔCDB(c.c.c)
⇒^ABD=^CDB;^ADB=^CBD;ˆA=ˆC .
Ta có: ^ABD và ^CDB là cặp góc so le trong bằng nhau nên AB // CD.
^ADB và ^CBD là cặp góc so le trong bằng nhau nên AD // BC.
Câu 14: Cho hình vẽ 
Khẳng định nào dưới đây là sai ?
Khẳng định nào dưới đây là sai ?
- A
- B
- C
- D
Xét ΔABC và ΔA′CB có {BCchungAC=A′BAB=A′C⇒ΔABC=ΔA′CB(c.c.c)⇒{^BA′C=90o^A′BC=^ACB
Câu 15: Cho tam giác ABC có ˆA=100o , AB = AC. Số đo góc ^ABC bằng:
- A
- B
- C
- D
Xét tam giác ΔABC cân tại A có ^BAC+^ABC+^ACB=180o.
⇒2^ABC=180o−^BAC=180o−100o=80o
⇒^ABC=80o:2=40o .
Câu 16: Cho hình vẽ bên 
Khẳng định đúng là
Khẳng định đúng là
- A
- B
- C
- D
Ta có {BA=BDAC=CDBCchung⇒ΔABC=ΔDBC(c−c−c)⇒^ABC=^DBC (2 góc tương ứng bằng nhau)
Mà CB nằm giữa BA và BD nên tia CB là tia phân giác góc ^ACD
Câu 17: ΔABC=ΔDBC(c.c.c) cần có những điều kiện nào?
- A
- B
- C
- D
ΔABC=ΔDBC(c.c.c)⇒{AB=DBAC=DCBCchung
Câu 18: Cho tam giác ABC có D là trung điểm của BC. Hỏi tam giác ABC cần thêm điều kiện gì để ΔABD=ΔACD(c.c.c).
- A
- B
- C
- D
/08.png)
Xét tam giác ABD và tam giác ACD có:
Cạnh chung AD;
BD = CD (Vì D là trung điểm của BC);
Vậy để ΔABD=ΔACD(c.c.c) thì cần có thêm AB = AC.
Câu 19: Cho tam giác ABC. Vẽ cung tròn tâm B có bán kính bằng AC, vẽ cung tròn tâm C có bán kính bằng AB, chúng cắt nhau ở D (D và B nằm khác phía đối với AC). Khi đó:
- A
- B
- C
- D
/10.png)
Vì cung tâm B bán kinh AC nên BD = AC.
Vì cung tâm C bán kính AB nên CD = AB.
Xét tam giác ABC và tam giác DCB có:
Cạnh chung BC; AB = CD; BD = AC.
⇒ΔABC=ΔDCB(c.c.c)
⇒^BAC=^BDC ; ^ABC=^DCB;^ACB=^DBC .
Câu 20: Chọn đáp án đúng. Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. Khi đó:
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. Khi đó:
- A
- B
- C
- D
/01.png)
Xét tam giác ABM và tam giác ACM có:
Cạnh chung AM;
AB = AC (giả thiết);
MB = MC (Vì M là trung điểm của BC)
⇒ΔABM=ΔACM (c.c.c).
⇒^BAM=^CAM ; ^ABM=^ACM .
Câu 21: Cho hình vẽ bên.
 Khẳng định nào sau đây là khẳng định sai?
Khẳng định nào sau đây là khẳng định sai?
 Khẳng định nào sau đây là khẳng định sai?
Khẳng định nào sau đây là khẳng định sai?- A
- B
- C
- D
Xét ΔABC và ΔCDA có {AB=DCBC=ADACchung⇒ΔABC=ΔCDA(c.c.c)⇒^BAC=^ACD⇒AB//CD
Câu 22: Cho ΔABC=ΔMNP(c.c.c) như hình vẽ 
Khẳng định nào dưới đây là đúng ?
Khẳng định nào dưới đây là đúng ?
- A
- B
- C
- D
Do ΔABC=ΔMNP(c.c.c)⇒{ˆB=ˆNˆA=ˆMAC=MP
Xem thêm các bài tiếp theo bên dưới