Hai đường thẳng vuông góc
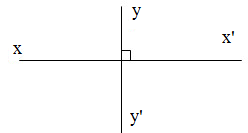
Lý thuyết về Hai đường thẳng vuông góc
1. Hai đường thẳng vuông góc
*Định nghĩa: Hai đường thẳng $xx'$ và $yy'$ cắt nhau và trong các góc tạo thành có một góc vuông được gọi là hai đường thẳng vuông góc và được kí hiệu là $xx' \bot yy'$
Khi $xx'$ và $yy'$ là hai đường thẳng vuông góc (và cắt nhau tại $O$) ta còn nói: đường thẳng $xx'$ vuông góc với đường thẳng $yy'$ (tại $O$) hoặc đường thẳng $yy'$ vuông góc với đường thẳng $xx'$ (tại $O$), hoặc hai đường thẳng $xx'$, $yy'$ vuông góc với nhau tại $O$.
*Tính chất: Có một và chỉ một đường thẳng $a'$ đi qua điểm $O$ và vuông góc với đường thẳng $a$ cho trước.
2. Đường trung trực của đoạn thẳng
*Định nghĩa: Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng ấy.
Khi $d$ là đường trung trực của đoạn thẳng $AB$ ta cũng nói: Hai điểm $A$ và $B$ đối xứng với nhau qua đường thẳng $d$.
Bài tập tự luyện có đáp án
Câu 1: Cho \(\angle \) xOy = 300. Vẽ
các góc yOz kề bù với \(\angle \)xOy. Vẽ \(\angle \)zOt = 600 sao
cho tia Ot nằm giữa hai tia Oz và Oy. Đường thẳng chứa tia Ot và đường thẳng
chứa tia Oy có đặc điểm gì?
- A
- B
- C
- D
Câu 2: Cho ba điểm A; B;C không
thẳng hàng, đoạn thẳng AB= 2 cm; BC = 3 cm , vẽ đường trung trực của đoạn thẳng
AB và BC. Hai đường trung trực :
- A
- B
- C
- D
- E
Câu 3: Cho $ \widehat{xOy} $ và $ \widehat{yOz} $ là hai góc kề bù. Tia Om là phân giác của $ \widehat{xOy} $ . Trên cùng một nửa mặt phẳng bờ xz chứa tia Oy, vẽ tia On sao cho: On vuông góc với Om. Khẳng định nào sau đây là đúng?
- A
- B
- C
- D
Do Om là phân giác của $ \widehat{xOy} $ nên $ \widehat{mOy}=\dfrac{1}{2}\widehat{xOy} $
Mà $ \widehat{xOy} $ và $ \widehat{y\text{O}z} $ là hai góc kề bù nên $ \widehat{xOy}+\widehat{y\text{O}z}=\widehat{xOz} $
Ta có $ \widehat{mOn}=\dfrac{1}{2}\widehat{xOz} $ hay $ \widehat{mOy}+\widehat{yOn}=\dfrac{1}{2}\widehat{xOz}=\Leftrightarrow \dfrac{1}{2}\widehat{xOy}+\widehat{y\text{On}}=\dfrac{1}{2}\left( \widehat{xOy}+\widehat{y\text{O}z} \right)\Rightarrow \widehat{y\text{On}}=\dfrac{1}{2}\widehat{yOz} $
Nên tia On là tia phân giác $ \widehat{yOz} $ .
Câu 4: Cho góc bẹt $ \widehat{xOy} $ . Vẽ tia $ Ot $ vuông góc với tia $ Ox $ . Góc $ \widehat{tOy} $ là:
- A
- B
- C
- D

Ta có $ \widehat{xOy} $ là góc bẹt $ \Rightarrow $ $ \widehat{xOy}={{180}^{o}} $ và tia $ Ox $ và tia $ Oy $ là hai tia đối nhau.
Vì tia $ Ot $ vuông góc với $ Ox $ nên $ \widehat{xOt}={{90}^{o}} $ .
Do đó: $ \widehat{tOy}=\widehat{xOy}-\widehat{xOt}={{180}^{o}}-{{90}^{o}}={{90}^{o}} $ .
Câu 5: Cho đoạn thẳng $ AB=8cm $ . Đường trung trực của đoạn thẳng $ AB $ cắt $ AB $ tại $ M $ . Khi đó:
- A
- B
- C
- D

Vì đường thẳng $ d $ là đường trung trực của $ AB $ nên $ M $ là trung điểm của $ AB $ $ \Rightarrow \,\,MA=MB=\dfrac{1}{2}AB=\dfrac{1}{2}.8=4\,(cm). $
Câu 6: Cho hai đường thẳng a và
b. Phát biểu nào sai
- A
- B
- C
- D
Câu 7: Cho góc bẹt $ \widehat{AOB} $ . Trên cùng một nửa mặt phẳng bờ AB, vẽ các tia OC, OD sao cho $ \widehat{AOC}={{60}^{o}},\widehat{BOD}={{30}^{o}} $ . Khẳng định sai là
- A
- B
- C
- D
Do $ \widehat{AOB} $ là góc bẹt nên $ \widehat{AOB}={{180}^{o}} $ mà $ \widehat{AOC}={{60}^{o}},\widehat{BOD}={{30}^{o}} $ nên $ \widehat{DOC}=\widehat{AOB}-\widehat{BO\text{D}}-\widehat{AOC}={{180}^{o}}-{{30}^{o}}-{{60}^{o}}={{90}^{o}} $
$ \widehat{BOC}=\widehat{AOB}-\widehat{AOC}={{180}^{o}}-{{60}^{o}}={{120}^{o}} $
$ \widehat{AO\text{D}}=\widehat{AOB}-\widehat{DOB}={{180}^{o}}-{{30}^{o}}={{150}^{o}} $
Câu 8: Hai đường thẳng xx’và yy’ cắt nhau tại O. Chúng
được gọi là hai đường thẳng vuông góc khi:
- A
- B
- C
- D
Câu 9: Cho các câu sau: (1) Hai đường thẳng vuông góc thì cắt nhau.
(2) Hai đường thẳng cắt nhau thì vuông góc.
(3) Mỗi đoạn thẳng có duy nhất một đường trung trực.
(4) Hai đường thẳng vuông góc tạo thành bốn góc vuông.
Số câu đúng là:
(1) Hai đường thẳng vuông góc thì cắt nhau.
(2) Hai đường thẳng cắt nhau thì vuông góc.
(3) Mỗi đoạn thẳng có duy nhất một đường trung trực.
(4) Hai đường thẳng vuông góc tạo thành bốn góc vuông.
Số câu đúng là:
- A
- B
- C
- D
- Theo định nghĩa ta có hai đường thẳng vuông góc thì cắt nhau và tạo thành bốn góc vuông.
- Mỗi đoạn thẳng có duy nhất một trung điểm nên có duy nhất một đường trung trực.
- Hai đường thẳng cắt nhau có thể không vuông góc (chẳng hạn hình vẽ)

Vậy trong các câu trên có 3 câu đúng là: (1), (3) và (4).
Câu 10: Đường thẳng AB cắt đoạn thẳng CD tại M. Đường
thẳng AB là đường trung trực của đoạn thẳng CD khi
- A
- B
- C
- D
Câu 11: Hai đường thẳng xx’ và
yy’ vuông góc với nhau tại O. Số góc tạo thành không có điểm trong chung là
- A
- B
- C
- D
- E
Câu 12: Cho hai đường thẳng xy và zt vuông góc với nhau tại O. Vẽ tia Om nằm giữa hai tia Ox, Oz sao cho $ \widehat{xOm}={{30}^{o}} $ , gọi On là tia đối của tia Om. Số đo góc $ \widehat{nOt} $ là
- A
- B
- C
- D
Ta có $ \widehat{xOm} $ và $ \widehat{y\text{O}n} $ là hai góc đối đỉnh nên $ \widehat{xOm}=\widehat{y\text{O}n}={{30}^{o}} $
Mà xy và zt vuông góc với nhau tại O nên $ \widehat{y\text{O}t}={{90}^{o}} $ hay $ \widehat{y\text{O}n}+\widehat{nOt}={{90}^{o}}\Rightarrow \widehat{nOt}={{60}^{o}} $
Câu 13: Chọn câu trả lời đúng nhất.Nếu đường thẳng xy là đường trung trực của đoạn
thẳng AB thì :
- A
- B
- C
- D
Câu 14: Cho Ox, Oy là hai tia đối nhau. Trên tia Ox lấy điểm M sao cho OM = 3cm, trên tia Oy lấy điểm N sao cho ON = 3cm. Qua O vẽ đường thẳng zt sao cho $ \widehat{xOz}=\widehat{yOz} $ . Khẳng định sai là
- A
- B
- C
- D
Do $ \widehat{xOz}=\widehat{yOz} $ mà $ \widehat{xOz} $ và $ \widehat{yOz} $ là hai góc kề bù nên $ \widehat{xOz}=\widehat{yOz}={{90}^{o}}\Rightarrow xy\bot zt $
Mà $ OM=ON=3cm\Rightarrow zt\bot MN $ nên zt là đường trung trực của đoạn MN
Câu 15: Trên cùng một nửa mặt phẳng có bờ chứa tia $ OA $ , vẽ các tia $ OB $ và $ OC $ sao cho $ \widehat{AOB}={{65}^{o}} $ ; $ OC $ vuông góc với $ OA $ . Số đo góc $ \widehat{BOC} $ bằng:
- A
- B
- C
- D

Vì tia $ OC $ vuông góc với tia $ OA $ nên $ \widehat{AOC}={{90}^{o}} $ .
Trên cùng một nửa mặt phẳng bờ chứa tia $ OA $ có: $ \widehat{AOB}={{65}^{o}}\, < \,\widehat{AOC}={{90}^{o}} $
$ \Rightarrow $ Tia $ OB $ nằm giữa hai tia $ OA $ và $ OC $
$ \Rightarrow \,\,\widehat{AOC}=\widehat{AOB}+\widehat{BOC} $
$ \Rightarrow \,\widehat{BOC}=\widehat{AOC}-\widehat{AOB}={{90}^{o}}-{{65}^{o}}={{25}^{o}}. $
Câu 16: Cho hai đường thẳng $ a $ và $ b $ vuông góc với nhau và cắt nhau tại $ O $ . Trên đường thẳng $ a $ lấy các điểm $ A,B $ phân biệt sao cho OA = OB. Trên đường thẳng $ b $ lấy các điểm $ C,D $ phân biệt sao cho OC = OD. Hỏi trong hình vẽ có bao nhiêu đường trung trực ?
- A
- B
- C
- D

Ta có: $ a\bot CD $ tại $ O $ và $ OC=OD $
$ \Rightarrow $ đường thẳng $ a $ là đường trung trực của đoạn thẳng CD.
$ b\bot AB $ tại $ O $ và $ OA=OB $
$ \Rightarrow $ đường thẳng $ b $ là đường trung trực của đoạn thẳng AB.
Câu 17: Trên tia $ Ax $ lấy hai điểm $ B $ và $ D $ sao cho $ AB=3cm,AD=7cm $ . Vẽ đường thẳng $ d $ là đường trung trực của $ BD $ . Khoảng cách từ trung điểm của đoạn thẳng $ BD $ đến mỗi đầu đoạn thẳng của $ BD $ là:
- A
- B
- C
- D

Trên tia $ Ax $ có $ AB=3cm\, < AD=7cm $
$ \Rightarrow $ Điểm $ B $ nằm giữa $ A $ và $ D $
$ \Rightarrow \,AD=AB+BD\Rightarrow \,\,BD=AD-AB=7cm-3cm=4cm. $
Gọi $ M $ là giao điểm của đường thẳng $ d $ và $ Ax $ .
Vì đường thẳng $ d $ là đường trung trực của đoạn thẳng $ BD $ nên $ M $ là trung điểm của $ BD $
$ \Rightarrow \,\,MB=MD=\dfrac{BD}{2}=\dfrac{4}{2}=2\,(cm). $
Câu 18: Cho $ \widehat{AOB}={{130}^{o}} $ . Trong góc $ \widehat{AOB} $ vẽ các tia $ OM $ , $ ON $ sao cho $ ON $ vuông góc với $ OA $ , $ OM $ vuông góc với $ OB $ . Khi đó:
- A
- B
- C
- D

Ta có: $ OA\bot ON\,\,\,\Rightarrow \,\,\widehat{AON}={{90}^{o}} $ .
$ OB\bot OM\Rightarrow \widehat{BOM}={{90}^{o}} $ .
Tia $ OM $ nằm giữa hai tia $ OA $ và $ OB $ $ \Rightarrow \,\widehat{AOB}=\widehat{BOM}+\widehat{AOM}\Rightarrow \,\widehat{AOM}=\widehat{AOB}-\widehat{BOM}={{130}^{o}}-{{90}^{o}}={{40}^{o}}. $
Tia $ ON $ nằm giữa hai tia $ OA $ và $ OB $ $ \Rightarrow \,\widehat{AOB}=\widehat{AON}+\widehat{BON}\Rightarrow \,\,\widehat{BON}=\widehat{AOB}-\widehat{AON}={{130}^{o}}-{{90}^{o}}={{40}^{o}} $ .
Vậy $ \widehat{AOM}=\widehat{BON}={{40}^{o}} $ .
Câu 19: Chọn câu phát biểu đúng
- A
- B
- C
- D
Câu 20: Cho $ \widehat{AOB}={{80}^{o}} $ , OC là tia phân giác của góc AOB .Gọi OD là tia đối của tia OB, OE là tia đối của tia OC . Trên nửa mặt phẳng bờ OD chứa tia OE, vẽ tia OM sao cho $ OM\bot OD $ . Số đo góc $ \widehat{EOM} $ là
- A
- B
- C
- D
Do OC là tia phân giác của góc AOB nên $ \widehat{AOC}=\widehat{COB}=\dfrac{1}{2}\widehat{AOB}={{40}^{o}} $
Lại có $ \widehat{BOC} $ và $ \widehat{EO\text{D}} $ là hai góc đối đỉnh nên $ \widehat{BOC}=\widehat{EO\text{D}}={{40}^{o}} $
Ta có $ \widehat{DOM}=\widehat{EO\text{D}}+\widehat{MOE}\Rightarrow \widehat{MOE}=\widehat{DOM}-\widehat{EO\text{D}}={{90}^{o}}-{{40}^{o}}={{50}^{o}} $
Câu 21: Cho $ \widehat{AOB}={{130}^{o}} $ . Vẽ tia $ OC $ nằm giữa hai tia $ OA $ và $ OB $ sao cho $ \widehat{AOC}={{40}^{o}} $ . Khi đó:
- A
- B
- C
- D

Vì tia $ OC $ nằm giữa hai tia $ OA $ và $ OB $ nên $ \widehat{AOB}=\widehat{AOC}+\widehat{BOC} $
$ \Rightarrow \,\,\widehat{BOC}=\widehat{AOB}-\widehat{AOC}={{130}^{o}}-{{40}^{o}}={{90}^{o}} $
$ \Rightarrow $ $ OB $ vuông góc với OC.
Câu 22: Vẽ hai đường thẳng $ xy $ và $ x'y' $ vuông góc với nhau và cắt nhau tại $ O $ . Kẻ tia $ Om $ là tia phân giác của $ \widehat{xOx'} $ . Khi đó $ \widehat{xOm} $ bằng :
- A
- B
- C
- D

Vì $ xy\bot x'y' $ tại O nên $ \widehat{xOx'}={{90}^{0}} $ .
Vì tia $ Om $ là tia phân giác của góc $ \widehat{xOx} $ nên $ \widehat{xOm}=\dfrac{1}{2}\widehat{xOx'}=\dfrac{1}{2}{{.90}^{0}}={{45}^{0}} $ .
Câu 23: Cho $ \widehat{MON}={{120}^{o}} $ , vẽ OP và OQ nằm giữa hai tia OM và ON sao cho $ OP\bot OM $ ; $ OQ\bot ON $ . Số đo $ \widehat{POQ} $ bằng
- A
- B
- C
- D
Do $ \left\{ \begin{array}{l} OP\bot OM \\ OQ\bot ON \end{array} \right.\Rightarrow \left\{ \begin{array}{l} \widehat{MOP}={{90}^{o}} \\ \widehat{NOQ}={{90}^{o}} \end{array} \right. $ mà $ \widehat{MON}={{120}^{o}} $ nên $ \left\{ \begin{array}{l} \widehat{MOQ}={{30}^{o}} \\ \widehat{PON}={{30}^{o}} \end{array} \right.\Rightarrow \widehat{POQ}={{60}^{o}} $
Câu 24: Cho I là trung điểm của
đoạn thẳng AB. Chọn câu trả lời đúng
- A
- B
- C
- D
- E
Câu 25: Cho $ \widehat{AOB}={{130}^{o}} $ . Về phía trong $ \widehat{AOB} $ vẽ tia OC sao cho $ OC\bot OA $ . Số đo góc $ \widehat{BOC} $ là
- A
- B
- C
- D
Ta có $ \widehat{BOC}=\widehat{AOB}-\widehat{AOC}={{130}^{o}}-{{90}^{o}}={{40}^{o}} $
Câu 26: Cho hình vẽ sau: 
Để vẽ được hình trên, bạn An vẽ theo từng bước nhưng thứ tự các bước cho dưới đây đã bị xáo trộn. Em hãy sắp xếp lại tuần tự các bước vẽ cho đúng.
(1) Qua $ M $ vẽ tia $ Mt $ vuông góc với tia $ Ox $ tại $ B $ .
(2) Vẽ góc $ \widehat{xOy} $ có số đo bằng $ {{60}^{o}} $ .
(3) Qua $ M $ vẽ tia $ Mz $ vuông góc với tia $ Oy $ tại $ A $ .
(4) Lấy điểm $ M $ bất kì trong góc $ \widehat{xOy} $ .
Thứ tự đúng là:

Để vẽ được hình trên, bạn An vẽ theo từng bước nhưng thứ tự các bước cho dưới đây đã bị xáo trộn. Em hãy sắp xếp lại tuần tự các bước vẽ cho đúng.
(1) Qua $ M $ vẽ tia $ Mt $ vuông góc với tia $ Ox $ tại $ B $ .
(2) Vẽ góc $ \widehat{xOy} $ có số đo bằng $ {{60}^{o}} $ .
(3) Qua $ M $ vẽ tia $ Mz $ vuông góc với tia $ Oy $ tại $ A $ .
(4) Lấy điểm $ M $ bất kì trong góc $ \widehat{xOy} $ .
Thứ tự đúng là:
- A
- B
- C
- D
Để được hình vẽ đã cho ta vẽ tuần tự theo các bước:
Bước 1: Vẽ góc $ \widehat{xOy} $ có số đo bằng $ {{60}^{o}} $ . (2)
Bước 2: Lấy điểm $ M $ bất kì trong góc $ \widehat{xOy} $ . (4)
Bước 3: Qua $ M $ vẽ tia $ Mt $ vuông góc với tia $ Ox $ tại $ B $ . (1)
Bước 4: Qua $ M $ vẽ tia $ Mz $ vuông góc với tia $ Oy $ tại $ A $ . (3)
(chú ý có thể vẽ bước 4 trước rồi vẽ bước 3)
Vậy thứ tự đúng là: (2), (4), (1), (3) hoặc (2), (4), (3), (1) .
Câu 27: Cho đường thẳng xy, lấy điểm O thuộc xy. Trên nửa mặt phẳng bờ xy vẽ hai tia Oa, Ob sao cho $ \widehat{xOa}=\widehat{yOb} < {{90}^{o}} $ , vẽ tia $ Om\bot xy $ . Khẳng định nào sau đây là đúng
- A
- B
- C
- D
Do $ Om\bot xy $ nên $ \widehat{xOm}=\widehat{mOy}={{90}^{o}} $ mà $ \widehat{xOa}=\widehat{yOb} $ nên $ \widehat{aOm}=\widehat{mOb}\Rightarrow $ Om là tia phân giác $ \widehat{aOb} $ .