Tính chất ba đường trung trực của tam giác
Lý thuyết về Tính chất ba đường trung trực của tam giác
Tính chất ba đường trung trực của tam giác
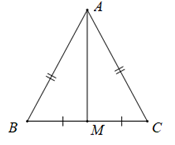
Định lí 1: Trong một tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến ứng với cạnh đáy này.
Định lí 2: Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó.
Trên hình, điểm $O$ là giao điểm của các đường trung trực của $\Delta ABC$. Ta có $OA=OB=OC$. Điểm $O$ là tâm đường tròn ngoại tiếp $\Delta ABC$
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác ABC với phân giác trong AD. Từ một điểm P thuộc đoạn DC, kẻ một đường thẳng song song với AD, cắt các đường thẳng AB và AC lần lượt tại M và N.
Chọn đáp án sai.
- A
- B
- C
- D

Vì $ MP//AD $ $ \Rightarrow {{\widehat{A}}_{1}}=\widehat{M} $ (hai góc ở vị trí đồng vị); $ {{\widehat{A}}_{2}}=\widehat{ANM} $ (hai góc ở vị trí so le trong).
Mà $ {{\widehat{A}}_{1}}={{\widehat{A}}_{2}}\Rightarrow \widehat{M}=\widehat{ANM}\Rightarrow \Delta AMN $ cân tại A.
$ \Rightarrow $ Đường trung trực của MN đi qua điểm A.
Câu 2: Cho tam giác ABC vuông tại A. Vẽ ra phía ngoài tam giác ABC các tam giác ABD và ACE lần lượt vuông cân tại D và E.
Chọn đáp án sai.
- A
- B
- C
- D

Vì $ \Delta ACE $ vuông cân tại E $ \Rightarrow \widehat{EAC}={{45}^{0}}. $
Vì $ \Delta ABD $ vuông cân tại D $ \Rightarrow \widehat{BAD}={{45}^{0}}. $
$ \Rightarrow \widehat{EAD}={{45}^{0}}+{{90}^{0}}+{{45}^{0}}={{180}^{0}}. $
Vậy ba điểm D, A, E thẳng hàng.
Câu 3: Cho tam giác ABC cân tại A. Hai đường trung trực của các cạnh AB và BC cắt nhau tại M. Trên cạnh AB lấy điểm D và trên cạnh AC lấy điểm E sao cho $ AD=CE. $
Chọn đáp án sai.
- A
- B
- C
- D

Vì $ \Delta ABC $ cân tại A nên đường trung trực của cạnh BC đi qua đỉnh A, và nó cũng đồng thời là đường phân giác góc của $ \Delta ABC $ .
$ \Rightarrow MA=MB=MC $ và $ {{\widehat{A}}_{1}}={{\widehat{A}}_{2}}. $ (1)
Vì $ MA=MC $ nên $ \Delta MAC $ cân tại M $ \Rightarrow {{\widehat{A}}_{2}}={{\widehat{C}}_{1}}. $ (2)
Từ (1) và (2) suy ra $ {{\widehat{A}}_{1}}={{\widehat{C}}_{1}}. $ Do vậy $ \Delta ADM=\Delta CEM\left( c.g.c \right)\Rightarrow MD=ME. $
Câu 4: Cho $ \Delta ABC $ có $ \widehat{B}-\widehat{C}={{40}^{0}} $ . Đường trung trực của $ BC $ cắt $ AC $ tại $ I $ . Số đo của $ \widehat{ABI} $ là
- A
- B
- C
- D
Ta có $ I $ nằm trên đường trung trực của $ BC $ nên $ BI=IC\,\,\Rightarrow \,\Delta IBC $ cân tại $ I\Rightarrow \widehat{IBC}=\widehat{C} $ .
Mà $ \widehat{ABI}\,+\,\,\widehat{IBC}\,\,=\widehat{B}\,\Rightarrow \widehat{ABI}\,=\,\widehat{B}\,-\,\widehat{IBC}\,=\widehat{B}\,\,-\,\widehat{C}\,={{40}^{0}} $ .
Câu 5: Cho $ \Delta ABC $ cân tại A. Đường trung tuyến $ AM $ cắt đường trung trực của $ AC $ tại $ K $ . Khẳng định nào sau đây là sai?
- A
- B
- C
- D
Ta có $ \Delta ABC $ cân tại $ A $ , trung tuyến $ AM $ nên $ BM=MC $ và $ AM $ cũng đồng thời là trung trực và là đường phân giác
$ \Rightarrow \,AM $ là đường trung trực của $ BC $ .
K là giao của 2 đường trung trực nên K cách đều các đỉnh của tam giác $ \Delta ABC $ .
Câu 6: Cho tam giác ABC vuông tại A, có $ AB > AC. $ Đường trung trực của cạnh huyền BC cắt AB tại D. M là một điểm tùy ý trên đoạn BD. Chọn đáp án đúng.
Chọn đáp án đúng.
- A
- B
- C
- D

Hạ $ DE\bot BC. $
Vì độ dài hình chiếu EB bằng độ dài hình chiếu EC.
$ \Rightarrow $ Độ dài đường xiên BD bằng độ dài đường xiên DC.
Mặt khác, độ dài hình chiếu AD nhỏ hơn độ dài hình chiếu AM (vì M nằm trên đoạn BD).
$ \Rightarrow $ Độ dài đường xiên CD nhỏ hơn độ dài đường xiên CM.
$ \Rightarrow BD < CM. $
Câu 7: Cho góc nhọn xOy và một điểm M nằm trong góc ấy. Từ M kẻ các đường thẳng vuông góc với MA, MB lần lượt xuống Ox, Oy. Gọi C là trung điểm của đoạn thẳng OM, P là trung điểm của đoạn thẳng AB.
Chọn đáp án sai.
- A
- B
- C
- D

Xét $ \Delta AOM $ vuông tại A có trung tuyến AC $ \Rightarrow AC=\dfrac{1}{2}OM $ (tính chất tam giác vuông) (1)
Xét $ \Delta BOM $ vuông tại B có trung tuyến BC $ \Rightarrow BC=\dfrac{1}{2}OM $ (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: $ AC=BC\Rightarrow \Delta ABC $ cân tại C.
$ \Rightarrow $ CP cũng đồng thời là đường trung trực của $ AB. $
Câu 8: Tam giác ABC cân tại A có $ AB=14cm. $ Đường trung trực của AB cắt cạnh AC ở E. Biết chu vi tam giác BEC bằng 24cm. Độ dài cạnh BC là
- A
- B
- C
- D

E thuộc đường trung trực AB nên $ AE=BE. $
Chu vi $ \Delta BEC $ bằng: $ BE+EC+BC=AE+EC+BC=AC+BC=14+BC. $
Chu vi $ \Delta BEC $ bằng 24cm nên $ BC=10cm. $
Câu 9: Cho tam giác ABC cân tại A. Đường trung tuyến AM cắt đường trung trực của AC tại K.
Chọn đáp án sai.
- A
- B
- C
- D

$ \Delta ABC $ cân tại A nên đường trung tuyến AM cũng là đường trung trực.
K là giao điểm của các đường trung trực của BC, AC nên $ KA=KB=KC. $
Câu 10: Cho tam giác ABC cân tại A. Đường trung trực của cạnh AC cắt tia CB tại D nằm ngoài đoạn thẳng BC. Trên tia đối của tia AD lấy điểm E sao cho $ AE=BD. $
Chọn đáp án sai.
- A
- B
- C
- D

Vì $ \Delta ABC $ cân tại A nên $ AB=AC $ và $ {{\widehat{B}}_{1}}={{\widehat{C}}_{1}}. $
Vì D thuộc đường trung trực của AC nên tam giác $\Delta DAC$ cân tại $D$. Suy ra $\widehat{DAC} = \widehat{C_1}$.
Vậy $\widehat{DAC} = \widehat{B_1}$ $\Rightarrow \widehat{DBA} = \widehat{EAC}$.
$ \Rightarrow \Delta ABD=\Delta CAE\left( c.g.c \right)\Rightarrow AD=CE. $
Câu 11: Trong các khẳng định sau, khẳng định nào sai?
(1) Đường trung trực của đoạn thẳng là tập hợp tất cả các điểm cách đều hai mút của đoạn thẳng đó.
(2) Trong tam giác cân, trọng tâm và điểm cách đều ba đỉnh trùng nhau.
(3) Đường tròn ngoại tiếp tam giác có tâm là giao điểm ba đường phân giác của tam giác đó.
(4) Trong tam giác đều, ba đường trung trực đồng thời cũng là ba đường trung tuyến, ba đường phân giác.
- A
- B
- C
- D
Trong tam giác đều, trọng tâm và điểm cách đều ba đỉnh trùng nhau.
Đường tròn ngoại tiếp tam giác có tâm là giao điểm ba đường trung trực của tam giác đó.
Câu 12: Cho tam giác ABC có $ \widehat{A} > {{90}^{0}}. $ Các đường trung trực của AB và của AC cắt nhau tại O và cắt BC theo thứ tự ở D và E. Nối AD, AE, OB, OC. Chọn đáp án đúng.
Chọn đáp án đúng.
- A
- B
- C
- D

OD là đường trung trực của AB nên $ DA=DB,OA=OB. $
$ \Rightarrow \Delta OAD=\Delta OBD\left( c.c.c \right). $
Tương tự $ \Delta OAE=\Delta OCE. $