Tính chất ba đường cao của tam giác
Lý thuyết về Tính chất ba đường cao của tam giác
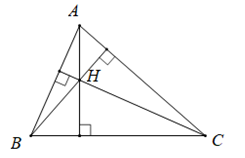
Định lí 1: Ba đường cao của một tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác.
Trên hình, là trực tâm của .
Định lí 2: Trong một tam giác cân, đường cao ứng với cạnh đáy đồng thời là đường phân giác, đường trung tuyến, đường trung trực của tam giác đó.
Nhận xét: Trong một tam giác, nếu có hai trong bốn loại đường (đường trung tuyến, đường phân giác, đường trung trực, đường cao) trùng nhau thì tam giác đó là tam giác cân.
Bài tập tự luyện có đáp án
Câu 1: Cho cân tại , đường trung tuyến . Qua kẻ đường thằng vuông góc với . Khẳng định nào dưới đây là đúng?
- A
- B
- C
- D
Do cân tại mà là đường trung tuyến
cũng đồng thời là đường cao
nên mà nên .
Câu 2: Cho đều, là trung điểm của . Gọi là trực tâm của . Độ dài bằng
- A
- B
- C
- D
Do đều nên vừa là trọng tâm, trực tâm cm.
Câu 3: Cho đều, đường trung tuyến . Gọi là trực tâm của , biết . Độ dài đoạn bằng
- A
- B
- C
- D
Do đều nên vừa là trọng tâm, trực tâm
Câu 4: Cho có . Trực tâm của là
- A
- B
- C
- D
Ta có vuông tại
Mà là trực tâm .
Câu 5: Đường cao hạ từ đỉnh của một tam giác cân khi biết đáy 5cm, cạnh bên 6,5cm có độ dài bằng
- A
- B
- C
- D

Ta có: (cạnh huyền-góc nhọn)
Áp dụng đị lý Py-ta-go vào vuông tại H có:
Câu 6: Cho tam giác ABC có , hai đường cao BE và CF. So sánh BE và CF.
- A
- B
- C
- D

Ta có:
Vì nên
Câu 7: Tam giác ABC cân tại B có chu vi 50cm, kẻ đường cao BH. Biết chu vi tam giác ABH bằng 40cm, độ dài BH bằng
- A
- B
- C
- D

Đặt
Ta có: (1)
Lại có: (2)
Từ (1) và (2) suy ra
Câu 8: Tam giác ABC cân tại A, có các đường cao BD, CE cắt nhau ở I, biết Số đo góc bằng
- A
- B
- C
- D

(cùng phụ ) nên
Câu 9: Cho tam giác ABC. Các tia phân giác của các góc ngoài đỉnh B và C gặp nhau ở K. Đường vuông góc với AK tại K cắt các đường thẳng AB, AC ở D và E. Chọn đáp án đúng.
Chọn đáp án đúng.
- A
- B
- C
- D

Ta có: các tia phân giác của các góc ngoài đỉnh B và C gặp nhau ở K.
AK là tia phân giác của góc A.
có đường cao cũng là đường phân giác nên là tam giác cân.
Câu 10: Độ dài đường cao của tam giác đều có cạnh 10cm bằng
- A
- B
- C
- D

Ta có: (cạnh huyền-góc nhọn)
Áp dụng đị lý Py-ta-go vào vuông tại H có:
Câu 11: Tam giác ABC cân tại A, tia phân giác của góc A cắt đường cao BD ở K.
Chọn khẳng định sai.
- A
- B
- C
- D

cân tại A, AK là tia phân giác của góc A nên AK cũng là đường cao.
cân tại A hiển nhiên
có AK, BD là đường cao nên K là trực tâm. Vậy
Câu 12: Tam giác ABC vuông tại A, đường cao AH.
Chọn khẳng định sai.
- A
- B
- C
- D

Trực tâm của tam giác vuông là đỉnh của góc vuông.
Câu 13: Cho đường tròn tâm O, dây AB có độ dài 6cm. Hạ tại H. Độ dài HB là
- A
- B
- C
- D

Vì OA=OB nên tam giác OAB cân tại O có OH là đường cao nên đồng thời là trung trực.
OH là đường trung trực của AB
Câu 14: Cho cân tại có và . Độ dài đường cao là
- A
- B
- C
- D
Ta có cân tại có là đường cao
Nên cũng đồng thời là đường trung tuyến.
Xét có (do là đường cao)
Áp dụng định lí pytago ta có: cm.
Câu 15: Cho tam giác ABC vuông cân tại A. Trên cạnh AB lấy điểm D, trên tia đối của tia AC lấy điểm E sao cho Gọi K là giao điểm của ED và BC. Chọn đáp án sai.
Chọn đáp án sai.
- A
- B
- C
- D

Ta thấy nên
có BA, EK là hai đường cao và cắt nhau ở D nên D là trực tâm tam giác ABC do đó