Quan hệ giữa ba cạnh của một tam giác, bất đẳng thức tam giá
Lý thuyết về Quan hệ giữa ba cạnh của một tam giác, bất đẳng thức tam giá
Quan hệ giữa ba cạnh của một tam giác, bất đẳng thức tam giác
Trong một tam giác, độ dài của một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng các độ dài của hai cạnh kia.
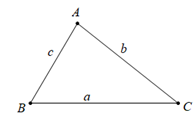
Ta có bất đẳng thức tam giác:
\[\left| AC-AB \right|<BC<AC+AB\] hay \[\left| b-c \right|<a<b+c\]
Bài tập tự luyện có đáp án
Câu 1: Bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho dưới đây không thể là ba cạnh của một tam giác ?
- A
- B
- C
- D
Trong một tam giác bộ ba cạnh có độ dài $ a,\,b,\,c $ thì phải thỏa mãn $ a < b+c $ .
Từ các phương án ta thấy: $ 4+3=7 $ nên bộ ba $ 4;7;3 $ không thể là ba cạnh của một tam giác. Còn các bộ ba cạnh còn lại đều thỏa mãn bất đẳng thức tam giác.
Câu 2: Cho tam giác cân $ ABC $ có $ BC=25cm,\text{ }AB=12cm $ . Khẳng định nào sau đây là đúng.
- A
- B
- C
- D
Xét tam giác $ ABC $ có
$ \begin{array}{l} BC+AB > AC > BC-AB\Leftrightarrow 25+12 > AC > 25-12 \\ \Leftrightarrow 37 > AC > 13 \end{array} $
Mà $ \Delta ABC $ cân nên $ \left[ \begin{array}{l} AC=AB \\ AC=BC \end{array} \right. $
$ \Rightarrow AC=25 $ . Vậy tam giác $ ABC $ cân tại $ C $ .
Câu 3: Chọn khẳng định đúng. Cạnh lớn nhất của một tam giác:
Cạnh lớn nhất của một tam giác:
- A
- B
- C
- D
Gọi a là độ dài cạnh lớn nhất của tam giác ABC, b và c là độ dài hai cạnh còn lại
$ (a\ge b\,;\,a\ge c) $ .
Theo bất đẳng thức tam giác: $ a < b+c. $
Cộng a vào hai vế: $ a+a < a+b+c\Rightarrow 2a < a+b+c\Rightarrow a < \dfrac{a+b+c}{2}. $
Vậy cạnh lớn nhất của một tam giác nhỏ hơn nửa chu vi tam giác.
Câu 4: Cho tam giác $ ABC $ có $ AB=5cm;\text{ }\,BC=9cm $ . Độ dài cạnh $ AC $ là một số nguyên. Biết chu vi tam giác $ ABC $ là bội của 6. Chu vi của tam giác $ ABC $ là
- A
- B
- C
- D
Xét tam giác $ ABC $
Ta có $ AB+BC > AC > BC-AB\Leftrightarrow 14 > AC > 4 $
$ 14+5+9 > AC+AB+BC > 5+9+4\Leftrightarrow 28 > AC+AB+BC > 18 $
Vậy chu vi tam giác $ ABC $ phải lớn hơn 18cm và nhỏ hơn 28cm.
Mà chu vi tam giác $ ABC $ là bội của 6.
Vậy chu vi tam giác $ ABC $ là 24 cm.
Câu 5: Cho tam giác ABC cân tại A, điểm D thuộc tia đối của tia BA. Khẳng định nào sau đây là đúng ?
- A
- B
- C
- D

Xét $ \Delta ADC:DC > AD-AC $ (theo bất đẳng thức tam giác).
Mà $ AB=AC $ (Vì $ \Delta ABC $ cân tại A).
Do đó: $ DC > AD-AB=DB. $
Câu 6: Cho tam giác $ ABC $ có $ AB=10cm,\text{ }\,AC=1cm $ , biết độ dài cạnh $ BC $ là một số nguyên. So sánh các góc của tam giác $ ABC $ ta được
So sánh các góc của tam giác $ ABC $ ta được
- A
- B
- C
- D
Ta có $ AB+AC > BC > \left| AB-AC \right|\Leftrightarrow 10+1 > BC > \left| 10-1 \right|\Leftrightarrow 11 > BC > 9 $
Mà độ dài cạnh $ BC $ là một số nguyên nên $ BC=10 $ .
Vậy tam giác $ ABC $ có $ AB=BC > AC\Rightarrow \widehat{C}=\widehat{A} > \widehat{B} $ ( quan hệ giữa góc và cạnh đối diện trong tam giác).
Câu 7: Tam giác ABC có $ AB=3dm,BC=27dm. $ Độ dài CA (tính bằng đề-xi-mét) là một số nguyên tố. Độ dài đoạn thẳng CA là:
- A
- B
- C
- D
Xét tam giác $ ABC $ ta có: $ \left| AB-BC \right| < CA < AB+BC $
$ \Rightarrow $ $ |27-3| < CA < 27+3\Rightarrow 24 < CA < 30. $
Mà độ dài CA là một số nguyên tố nên $ CA=29dm. $
Câu 8: Biết hai cạnh của một tam giác cân là 3,9cm và 7,9cm. Khi đó chu vi tam giác bằng:
- A
- B
- C
- D
Cạnh thứ ba của tam giác bằng một trong hai cạnh kia.
Áp dụng bất đẳng thức tam giác:
Loại trường hợp cạnh thứ ba bằng 3,9cm vì \[ 3,9+3,9 < 7,9. \]
Trường hợp cạnh thứ ba bằng 7,9cm thỏa mãn bất đẳng thức tam giác vì \[ 7,9 < 7,9+3,9. \]
Vậy chu vi tam giác là: \[ 7,9+7,9+3,9=19,7\left( cm \right). \]
Câu 9: Cho tam giác $ RSK $ có $ RS=~8cm,\text{ }\,SK=1cm $ , biết độ dài cạnh $ RK $ là một số nguyên. Chu vi tam giác $ RSK $ là
Chu vi tam giác $ RSK $ là
- A
- B
- C
- D
Ta có $ RS+SK > KR > \left| RS-SK \right|\Leftrightarrow 8+1 > KR > \left| 8-1 \right|\Leftrightarrow 9 > KR > 7 $
độ dài cạnh $ KR $ là một số nguyên nên $ KR=8 $ .
Vậy chu vi tam giác $ RSK $ là $ 8+1+8\text{ }=17 $ .
Câu 10: Cho tam giác ABC, có $ AB=15cm,\,\,BC=8cm. $ Tính độ dài cạnh AC, biết độ dài này (theo đơn vị xăng-ti-mét) là một số nguyên tố lớn hơn bình phương của 4. Chọn phương án đúng nhất.
Chọn phương án đúng nhất.
- A
- B
- C
- D
Xét $ \Delta ABC $ có: $ \left| AB-BC \right| < AC < AB+BC\Leftrightarrow \left| 15-8 \right| < AC < 15+8\Leftrightarrow 7 < AC < 23. $
Mà $ AC > {{4}^{2}}=16 $ và AC là số nguyên tố (giả thiết) nên $ AC=17cm $ hoặc $ AC=19cm. $
Câu 11: Độ dài ba cạnh của tam giác tỉ lệ với các số $ 2\,;\,3\,;4. $ Độ dài cạnh lớn nhất của tam giác bằng bao nhiêu nếu tổng độ dài hai cạnh kia là 20 ?
- A
- B
- C
- D
Gọi độ dài ba cạnh của tam giác là a, b, c.
Không mất tính tổng quát, ta giả sử: $ a\le b\le c. $
Từ giả thiết, ta có: $ \dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}. $
Với $ a+b=20 $ , thì áp dụng tính chất dãy tỉ số bằng nhau, ta có:
$ \dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b}{2+3}=\dfrac{20}{5}=4\Rightarrow c=16. $
Câu 12: Cho tam giác $ ABC $ vuông tại $ A $ có $ AB=x,\text{ }\,AC=y $ . Đẳng thức đúng là
- A
- B
- C
- D
Xét tam giác $ ABC $ vuông tại $ A $
Ta có $ B{{C}^{2}}=A{{B}^{2}}+A{{C}^{2}}\Rightarrow BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=\sqrt{{{x}^{2}}+{{y}^{2}}} $
$ AB+AC > BC $ hay $ x+y > \sqrt{{{x}^{2}}+{{y}^{2}}} $ .
Câu 13: Tam giác ABC có $ AB=1m,AC=3m. $ Độ dài BC (tính bằng mét) là một số tự nhiên. Độ dài đoạn thẳng BC là:
- A
- B
- C
- D
Xét tam giác $ ABC $ ta có: $ \left| AB-AC \right| < BC < AB+AC $
$ \Rightarrow $ $ |1-3| < BC < 3+1\Rightarrow 2 < BC < 4\Rightarrow BC=3. $
Vậy $ BC=3m. $
Câu 14: Cho bộ ba đoạn thẳng có độ dài tương ứng là a, b, c sao cho:
- Trường hợp 1: $ a=2b,b=2c. $
- Trường hợp 2: $ a=\dfrac{3}{2}b,b=\dfrac{3}{2}c. $
Hỏi có thể tồn tại tam giác từ ba đoạn thẳng đó trong mỗi trường hợp không ?
- A
- B
- C
- D
- Xét trường hợp 1: $ a=2b,b=2c. $
Giả sử tồn tại tam giác như vậy thì độ dài ba cạnh là c, 2c, 4c, mâu thuẫn với bất đẳng thức tam giác, vì $ c+2c < 4c. $ Vậy không tồn tại tam giác như vậy.
- Xét trường hợp 2: $ a=\dfrac{3}{2}b,b=\dfrac{3}{2}c. $
Cho $ c=1\Rightarrow b=\dfrac{3}{2}\,\,;\, $ $ a=\dfrac{3}{2}.\dfrac{3}{2}=\dfrac{9}{4}. $
Vì $ \dfrac{9}{4} < \dfrac{3}{2}+1 $ nên tồn tại tam giác.
Vậy có tồn tại tam giác trong trường hợp 2.
Câu 15: Tam giác ABC có $ AB=c,AC=b. $ Gọi M là trung điểm của BC. Chọn khẳng định đúng.
Chọn khẳng định đúng.
- A
- B
- C
- D

Trên tia đối của tia MA lấy điểm D sao cho $ MD=MA. $
$ \Delta DMC=\Delta AMB\left( c.g.c \right)\Rightarrow DC=AB=c. $
Xét $ \Delta ACD $ có $ AD < AC+DC\Rightarrow 2AM < b+c\Rightarrow AM < \dfrac{b+c}{2}. $