Tâm vị tự của hai đường tròn
Lưu về Facebook:
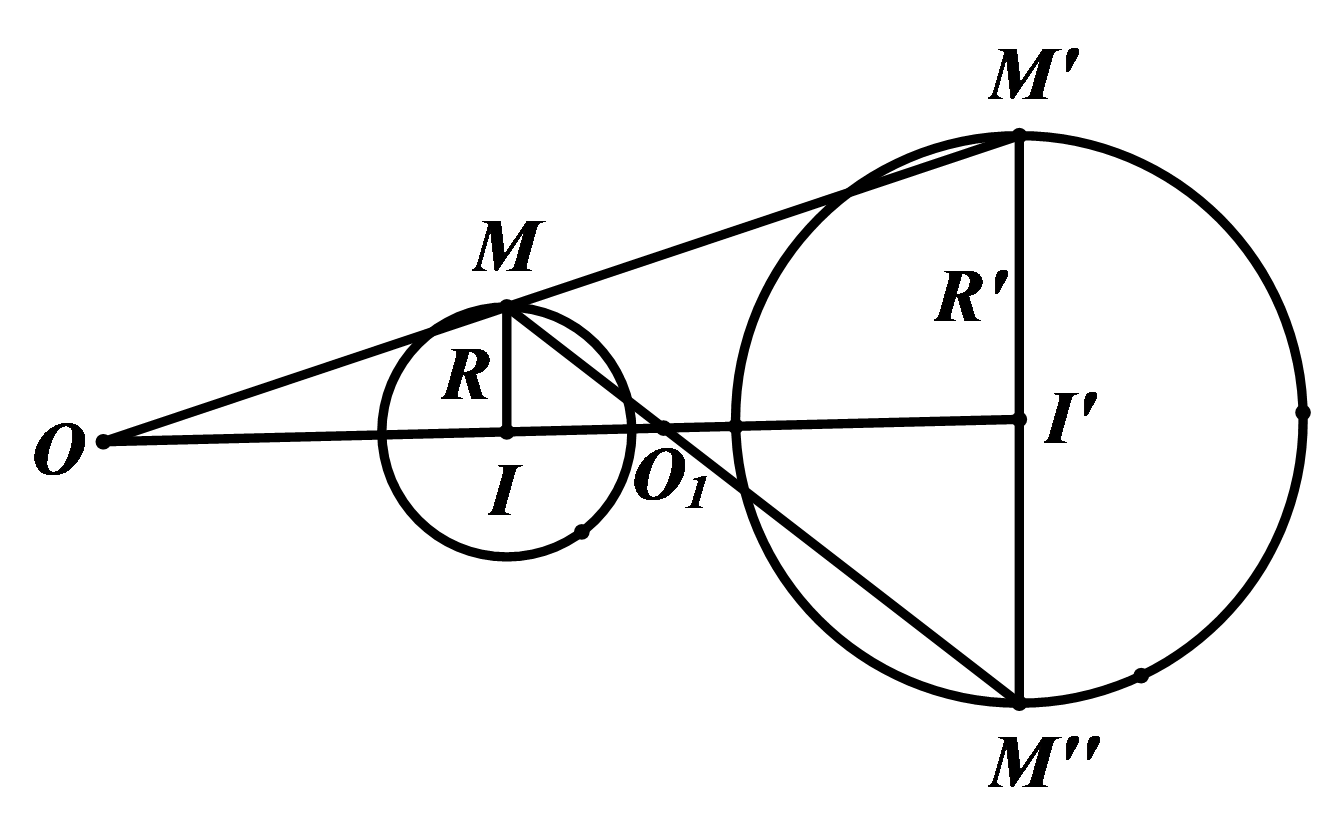
Lý thuyết về Tâm vị tự của hai đường tròn
Tâm vị tự của hai đường tròn
Định lí: Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia.
Tâm của phép vị tự này được gọi là tâm vị tự của hai đường tròn.
Cho hai đường tròn (I;R) và (I′;R′)
- Nếu I≡I′ thì các phép vị tự V(I;±R′R)biến (I;R) thành(I′;R′).
- Nếu I≠I′ và R≠R′ thì các phép vị tự V(O;R′R) và V(O1;−R′R) biến (I;R) thành(I′;R′). Ta gọi O là tâm vị tự ngoài còn O1 là tâm vị tự trong của hai đường tròn.
- Nếu Nếu I≠I′ và R=R′ thì có V(O1;−1) biến (I;R) thành(I′;R′).
Bài tập tự luyện có đáp án
Câu 1: Trong mặt phẳng Oxy cho đường tròn (C ):x2+y2−4x+6y−1=0 . Gọi (C′) là ảnh của đường tròn qua phép đồng dạng có được khi thực hiện liên tiếp phép quay tâm O góc quay 900 và phép V(O,−3) . Khi đó tâm của (C′) là
- A
- B
- C
- D
I(2;−3) là tâm của (C)
I′=Q(O,900)(I)⇒I′(3;2)
Gọi I″=V(O,−3)(I′)⇒I″(−9;−6)
Vậy (C′) có tâm (−9;−6).
Câu 2: Trong mặt phẳng Oxy, cho điểm M(3;−6) . Gọi N là ảnh của M qua phép đồng dạng có được từ việc thực hiện liên tiếp phép vị tự tâm O tỉ số −13 và phép đối xứng qua trục Oy. Tọa độ của N là:
- A
- B
- C
- D
Gọi M′(x′;y′)=V(O,−13)(M)⇒→OM′=−13→OM⇔{x′=−13.3y′=−13.(−6)⇔M′(−1;2)
N(x;y)=DOy(M′)⇒N(1;2)
N(x;y)=DOy(M′)⇒N(1;2)
Câu 3: Cho đường tròn (C) tâm I(1;−1) , bán kính R=2 . Đường tròn (S) là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số −2 và phép tịnh tiến theo vectơ →v(−1;2) . Khi đó (S) có:
- A
- B
- C
- D
Gọi I′(x′;y′) và R′ là tâm và bán kính của đường tròn (C′) là ảnh của (C) qua phép vị tự tâm O tỉ số −2 . Ta có
→OI′=k→OI⇔I′(−2;2),R′=2R=4
Gọi I″(x″;y″),R″ là tâm và bán kính của (C′) qua phép tịnh tiến theo vectơ →v(−1;2) thì I″(−3;4);R″=R′=4
Vậy đường tròn (S) có tâm (−3;4) bán kính R=4
→OI′=k→OI⇔I′(−2;2),R′=2R=4
Gọi I″(x″;y″),R″ là tâm và bán kính của (C′) qua phép tịnh tiến theo vectơ →v(−1;2) thì I″(−3;4);R″=R′=4
Vậy đường tròn (S) có tâm (−3;4) bán kính R=4