Dạng toán về giao tuyến của 2 mặt chứa 2 đường //
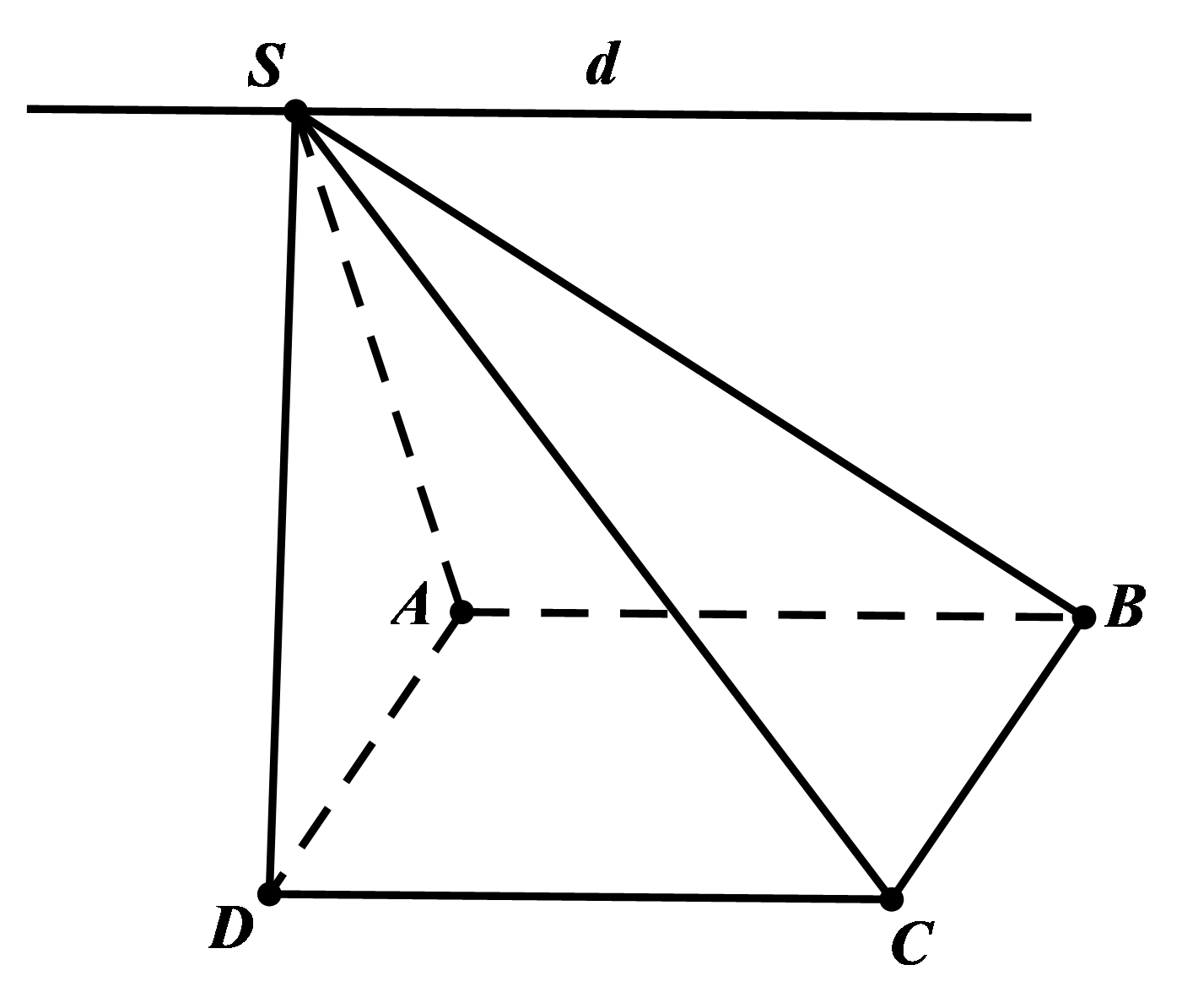
Lý thuyết về Dạng toán về giao tuyến của 2 mặt chứa 2 đường //
Phương pháp xác định giao tuyến của 2 mặt phẳng chứa 2 đường thẳng song song
Sử dụng tính chất: Nếu hai mặt phẳng \[\left( \alpha \right)\] và \[\left( \beta \right)\] có điểm chung \[M\]và lần lượt chứa hai đường thẳng song song \[d\] và \[d'\] thì giao tuyến của \[\left( \alpha \right)\] và \[\left( \beta \right)\] là đường thẳng đi qua \[M\] song song với \[d\] và \[d'\].
Ví dụ: Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành.
Tìm giao tuyến của hai mặt phẳng \[\left( SAB \right)\] và \[\left( SCD \right)\]
Lời giải:
Ta có \[\left\{ \begin{array}{l}
AB \subset \left( {SAB} \right)\\
CD \subset \left( {SCD} \right)\\
AB\parallel CD\\
S \in \left( {SAB} \right) \cap \left( {SCD} \right)
\end{array} \right.\]
\[\Rightarrow \left( SAB \right)\cap \left( SCD \right)=d\parallel AB\parallel CD,S\in d\].
Bài tập tự luyện có đáp án
Câu 1: Cho hình chóp $S.ABCD$ đáy là hình bình hành, gọi $M$ là điểm thuộc $SC$ sao cho $SM=\dfrac{2}{3}SC$. Gọi $N$ là giao điểm của $SD$ và $mp\left( MAB \right)$. Khi đó vị trí tương đối của $MN$ và $CD$ là
- A
- B
- C
- D
Vì $SD\subset \left( SCD \right)$ nên ta sẽ tìm giao tuyến của 2 mặt phẳng $\left( MAB \right)$,$\left( SCD \right)$, sau đó tìm giao điểm của $SD$ với giao tuyến thì đó là điểm N cần tìm.
\[M \in \left( {MAB} \right) \cap \left( {SCD} \right);AB \subset \left( {MAB} \right),CD \subset \left( {SCD} \right);AB//CD\]
$\Rightarrow $ giao tuyến của 2 mp là đường thẳng \[x\] qua \[M\] và song song với \[AB\] và \[CD\]. Khi đó \[x\] cắt \[SD\] tại \[N\] là giao điểm của $SD$ và \[mp\left( {MAB} \right)\]
Theo cách xác định giao tuyến trên ta có \[MN\,//CD.\]