Bài toán va chạm
Lý thuyết về Bài toán va chạm
1. Định luật bảo toàn động lượng của hệ cô lập.
- Động lượng của một hệ cô lập là một đại lượng bảo toàn.
$\overrightarrow{{{p}_{1}}}+\overrightarrow{{{p}_{2}}}+...+\overrightarrow{{{p}_{n}}}=h/s$
- Biểu thức của định luật ứng với hệ cô lập gồm hai vật m1 và m2.
${{m}_{1}}\overrightarrow{{{v}_{1}}}+{{m}_{2}}\overrightarrow{{{v}_{2}}}={{m}_{1}}\overrightarrow{{{v}_{1}}'}+{{m}_{2}}\overrightarrow{{{v}_{2}}'}$
${{m}_{1}}\overrightarrow{{{v}_{1}}}$ và ${{m}_{2}}\overrightarrow{{{v}_{2}}}$ là động lượng của vật 1 và vật 2 trước tương tác.
${{m}_{1}}\overrightarrow{{{v}_{1}}'}$ và ${{m}_{2}}\overrightarrow{{{v}_{2}}'}$ là động lượng của vật 1 và vật 2 sau tương tác.
2. Va chạm mềm.
Xét một vật khối lượng\[{{m}_{1}}\], chuyển động trên một mặt phẳng ngang với vận tốc $\overrightarrow{{{v}_{1}}}$ đến va chạm vào một vật có khối lượng \[{{m}_{2}}\] đang đứng yên. Sau va chạm hai vật nhập làm một và cùng chuyển động với vận tốc $\overrightarrow{v}$
Theo định luật bảo toàn động lượng ta có :
${{m}_{1}}\overrightarrow{{{v}_{1}}}=\left( {{m}_{1}}+{{m}_{2}} \right)\overrightarrow{v}$
suy ra $\overrightarrow{v}=\dfrac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}\overrightarrow{{{v}_{1}}}$
Va chạm của hai vật như vậy gọi là va chạm mềm.
Bài tập tự luyện có đáp án
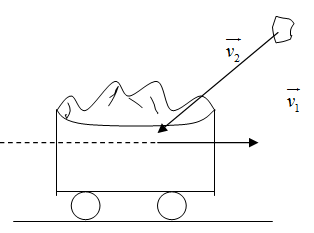
Câu 1: Một xe chở cát có khối lượng $ { m _ 1 }=390kg $ đang chuyển động theo phương ngang với vận tốc $ { v _ 1 }=8m/s $ , thì một hòn đá có khối lượng $ { m _ 2 }=10kg $ bay theo phương hợp với phương ngang 1 góc $ {{60}^ 0 } $ ngược chiều với vận tốc $ { v _ 2 }=12m/s $ đến cắm vào xe cát. Vận tốc của xe sau khi hòn đá rơi vào là:
- A
- B
- C
- D

Xét hệ gồm xe và hòn đá là hệ kín.
Chọn chiều dương là chiều chuyển động của xe.
Động lượng của hệ trước va chạm là: $ \overrightarrow p ={ m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }} $
Động lượng của hệ sau va chạm là: $ \overrightarrow p '=({ m _ 1 }+{ m _ 2 })\overrightarrow{v'} $
Định luật bảo toàn động lượng: $ \overrightarrow p =\overrightarrow p '\Leftrightarrow { m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }}=({ m _ 1 }+{ m _ 2 })\overrightarrow v '\quad \left( * \right) $
Chiếu (*) lên phương chuyển động nằm ngang:
$ \begin{array}{l} & { m _ 1 }{ v _ 1 }-{ m _ 2 }.{ v _ 2 }.\cos {{60}^ 0 }=({ m _ 1 }+{ m _ 2 })v' \\ & \Rightarrow v'=\dfrac{{ m _ 1 }{ v _ 1 }-{ m _ 2 }.{ v _ 2 }.c\text{os}{{60}^ 0 }}{{ m _ 1 }+{ m _ 2 }}=\dfrac{390.8-10.12.c\text{os}{{60}^ 0 }}{390+10}=7,65m/s \\ \end{array} $
Câu 2: Hai xe lăn nhỏ có khối lượng $ { m _ 1 }=300g $ và $ { m _ 2 }=2kg $ chuyển động trên mặt phẳng nằm ngang ngược chiều nhau với tốc độ tương ứng $ { v _ 1 }=2m/s $ và $ { v _ 2 }=0,8m/s $ . Sau khi va chạm hai xe dính vào nhau và chuyển động cùng vận tốc. Bỏ qua sức cản. Tốc độ của hai xe sau va chạm là
- A
- B
- C
- D
Chọn chiều dương là chiều chuyển động của xe 1.
+ Trước va chạm:
- Động lượng xe 1 là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=0,3.2=0,6\left( kg.m/s \right). $
- Động lượng của xe 2 là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=2.\left( -0,8 \right)=-1,6\left( kg.m/s \right) $
- Tổng động lượng của hệ trước va chạm là: $ p={ p _ 1 }+{ p _ 2 }=0,6-1,6=-1\left( kg.m/s \right) $
+ Sau khi va chạm hai xe dính vào nhau và chuyển động cùng vận tốc v, ta có:
$ p'=\left( { m _ 1 }+{ m _ 2 } \right)v=\left( 0,3+2 \right).v=2,3v\left( kg.m/s \right) $
Áp dụng định luật bảo toàn động lượng, ta có: p = p’
$ \Leftrightarrow -1=2,3v\Rightarrow v=-0,43(m/s) $
Sau va chạm, 2 vật cùng chuyển động với tốc độ 0,43 m/s ngược chiều dương đã chọn.
Câu 3: Trong va chạm mềm, đại lượng vật lí được bảo toàn là:
- A
- B
- C
- D
Trong va chạm mềm, động lượng được bảo toàn.
Câu 4: Hai xe lăn nhỏ có khối lượng $ { m _ 1 }=300g $ và $ { m _ 2 }=2kg $ chuyển động trên mặt phẳng nằm ngang cùng chiều nhau với tốc độ tương ứng $ { v _ 1 }=2m/s $ và $ { v _ 2 }=0,8m/s $ . Sau khi va chạm hai xe dính vào nhau và chuyển động cùng vận tốc. Bỏ qua sức cản. Tốc độ của hai xe sau va chạm là
- A
- B
- C
- D
+ Trước va chạm:
- Động lượng xe 1 là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=0,3.2=0,6\left( kg.m/s \right). $
- Động lượng của xe 2 là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=2.0,8=1,6\left( kg.m/s \right) $
- Tổng động lượng của hệ trước va chạm là: $ p={ p _ 1 }+{ p _ 2 }=0,6+1,6=2,2\left( kg.m/s \right) $
+ Sau khi va chạm hai xe dính vào nhau và chuyển động cùng vận tốc v, ta có:
$ p'=\left( { m _ 1 }+{ m _ 2 } \right)v=\left( 0,3+2 \right).v=2,3v\left( kg.m/s \right) $
Áp dụng định luật bảo toàn động lượng, ta có: p = p’
$ \Leftrightarrow 2,2=2,3v\Rightarrow v=0,96(m/s) $
Sau va chạm, 2 vật cùng chuyển động với tốc độ 0,96 m/s ngược chiều dương đã chọn.
Câu 5: Vật 1 chuyển động với vận tốc v đến va chạm và dính vào vật 2 đang đứng yên. Sau va chạm, hiện tượng như thế nào?
- A
- B
- C
- D
Áp dụng định luật bảo toàn động lượng: $ { m _ 1 }\overrightarrow v =({ m _ 1 }+{ m _ 2 })\overrightarrow{v'} $
Sau va chạm, hai vật chuyển động cùng chiều vật 1.
Câu 6: Một chiếc xe A đang chạy trên đường ngang có động lượng là 30 kgm/s, tới va chạm vào một chiếc xe B đang đang chuyển động với động lượng 40 kg.m/s theo hướng hợp với hướng chuyển động của xe A một góc $ {{60}^ 0 } $ . Sau va chạm, hai xe dính vào nhau và cùng chuyển động. Động lượng của 2 xe sau va chạm là:
- A
- B
- C
- D
Ta có: $ { p _ 1 }=30kg.m/s;{ p _ 2 }=40kg.m/s $
Coi hệ là kín. Áp dụng định luật bảo toàn động lượng ta có: $ \overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }}=\overrightarrow p $
$ \begin{array}{l} & \left( \widehat{\overrightarrow{{ p _ 1 }};\overrightarrow{{ p _ 2 }}} \right)={{60}^ 0 } \\ & \Rightarrow p=\sqrt{{{\left( { p _ 1 } \right)}^ 2 }+{{\left( { p _ 2 } \right)}^ 2 }+2{ p _ 1 }.{ p _ 2 }.c\text{os}{{60}^ 0 }} \\ & =\sqrt{{{\left( 30 \right)}^ 2 }+{{\left( 40 \right)}^ 2 }+2.30.40.c\text{os}{{60}^ 0 }}=10\sqrt{37}\left( kg.m/s \right) \\ \end{array} $
Câu 7: Một người khối lượng m1 = 60 kg đứng trên một xe goòng khối lượng m2 = 240 kg đang chuyển động trên đường ray với vận tốc 2 m/s. Tính vận tốc của xe nếu người nhảy về phía sau xe với vận tốc 4 m/s đối với xe (lúc sau)
- A
- B
- C
- D
Xét hệ: Xe + người là hệ kín.
Chọn chiều dương là chiều chuyển động ban đầu của xe.
Động lượng của hệ trước khi người nhảy là: $ p=\left( { m _ 1 }+{ m _ 2 } \right).{ v _ 1 } $
Động lượng của hệ sau khi người nhảy là:
$ \overrightarrow{p'}={ m _ 1 }\overrightarrow{{ v _ 1 }'}+{ m _ 2 }\overrightarrow{{ v _ 2 }'} $
Trong đó, $ \overrightarrow{{ v _ 2 }'} $ là vận tốc của xe sau khi người nhảy.
Người nhảy về phía sau xe nên vận tốc nhảy của người là: $ { v _ 1 }'={ v _ 2 }'-4\left( m/s \right) $
$ \Rightarrow p'={ m _ 1 }\left( { v _ 2 }'-4 \right)+{ m _ 2 }{ v _ 2 }' $
Áp dụng định luật bảo toàn động lượng cho hệ vật ta có: $ \overrightarrow p =\overrightarrow{p'} $
$ \begin{array}{l} & \left( { m _ 1 }+{ m _ 2 } \right).{ v _ 1 }={ m _ 1 }\left( { v _ 2 }'-4 \right)+{ m _ 2 }{ v _ 2 }'\Leftrightarrow \left( 60+240 \right).2=60.\left( { v _ 2 }'-4 \right)+240.{ v _ 2 }' \\ & \Rightarrow { v _ 2 }'=\dfrac{\left( 60+240 \right).2+60.4}{60+240}=2,8(m/s) \\ \end{array} $
Câu 8: Một vật có khối lượng 25kg rơi nghiêng một góc $ {{60}^ 0 } $ so với đường nằm ngang với vận tốc 36km/h vào 1 xe goòng chứa cát đứng trên đường ray nằm ngang. Cho khối lượng xe 975kg. Vận tốc của xe goòng sau khi vật cắm vào là:
- A
- B
- C
- D

v1 = 36km/h = 10 m/s
Động lượng của hệ lúc đầu: $ \overrightarrow{{ p _ 1 }}={ m _ 1 }\overrightarrow{{ v _ 1 }} $
Động lượng của hệ ngay sau khi vật rơi vào xe: $ \overrightarrow{{ p _ 2 }}=({ m _ 1 }+{ m _ 2 })\overrightarrow{{ v _ 2 }} $
Định luật bảo toàn động lượng: $ \overrightarrow{{ p _ 1 }}=\overrightarrow{{ p _ 2 }}\Leftrightarrow { m _ 1 }\overrightarrow{{ v _ 1 }}=({ m _ 1 }+{ m _ 2 })\overrightarrow{{ v _ 2 }}\quad \left( * \right) $
Chiếu (*) lên phương chuyển động nằm ngang:
$ \begin{array}{l} & { m _ 1 }{ v _ 1 }c\text{os}\alpha =({ m _ 1 }+{ m _ 2 }){ v _ 2 } \\ & \Rightarrow { v _ 2 }=\dfrac{{ m _ 1 }{ v _ 1 }c\text{os}\alpha }{{ m _ 1 }+{ m _ 2 }}=\dfrac{25.10.0,5}{25+975}=0,125m/s \\ \end{array} $
Câu 9: Viên bi A có khối lượng $ { m _ 1 }=60g $ chuyển động với vận tốc $ { v _ 1 }=5m/s $ va chạm vào viên bi B có khối lượng $ { m _ 2 }=40g $ chuyển động ngược chiều với vận tốc v2. Sau va chạm, hai viên bi đứng yên. Tốc độ của viên bi B là:
- A
- B
- C
- D
Chọn chiều dương là chiều chuyển động của viên bi A.
+ Trước va chạm:
- Động lượng của bi A là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=0,06.5=0,3\left( kg.m/s \right). $
- Động lượng của viên bi B là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=0,04.{ v _ 2 } $
- Tổng động lượng của hệ trước va chạm là: $ p={ p _ 1 }+{ p _ 2 }=0,3+0,04.{ v _ 2 } $
+ Sau va chạm hai viên bi đứng yên nên tổng động lượng của hệ bằng 0: p’ = 0.
Áp dụng định luật bảo toàn động lượng, ta có: p = p’
$ \Leftrightarrow 0,3+0,04.{ v _ 2 }=0\Rightarrow { v _ 2 }=-7,5(m/s) $
Trước va chạm, bi B chuyển động ngược chiều với bi A với tốc độ 7,5 m/s.
Câu 10: Một người khối lượng m1 = 60kg đứng trên một xe goòng khối lượng m2 = 240kg đang chuyển động trên đường ray với vận tốc 2m/s. Tính vận tốc của xe nếu người nhảy về phía trước xe với vận tốc 4m/s đối với xe (lúc sau)
- A
- B
- C
- D
Xét hệ: Xe + người là hệ kín.
Chọn chiều dương là chiều chuyển động ban đầu của xe.
Động lượng của hệ trước khi người nhảy là: $ p=\left( { m _ 1 }+{ m _ 2 } \right).{ v _ 1 } $
Động lượng của hệ sau khi người nhảy là:
$ \overrightarrow{p'}={ m _ 1 }\overrightarrow{{ v _ 1 }'}+{ m _ 2 }\overrightarrow{{ v _ 2 }'} $
Trong đó, $ \overrightarrow{{ v _ 2 }'} $ là vận tốc của xe sau khi người nhảy.
Người nhảy về phía trước xe nên vận tốc nhảy của người là: $ { v _ 1 }'={ v _ 2 }'+4\left( m/s \right) $
$ \Rightarrow p'={ m _ 1 }\left( { v _ 2 }'+4 \right)+{ m _ 2 }{ v _ 2 }' $
Áp dụng định luật bảo toàn động lượng cho hệ vật ta có: $ \overrightarrow p =\overrightarrow{p'} $
$ \begin{array}{l} & \left( { m _ 1 }+{ m _ 2 } \right).{ v _ 1 }={ m _ 1 }\left( { v _ 2 }'+4 \right)+{ m _ 2 }{ v _ 2 }'\Leftrightarrow \left( 60+240 \right).2=60.\left( { v _ 2 }'+4 \right)+240.{ v _ 2 }' \\ & \Rightarrow { v _ 2 }'=\dfrac{\left( 60+240 \right).2-60.4}{60+240}=1,2(m/s) \\ \end{array} $
Câu 11: Hai xe nhỏ khối lượng lần lượt là m1 và m2 đặt trên mặt bàn (hình vẽ). Một sợi dây mảnh luồn qua một lò xo để nối hai xe ép chặt lò xo. Hai đầu lò xo tì lên thành của hai xe. Người ta đốt cháy sợi dây. Tỉ số vận tốc của hai xe là:


- A
- B
- C
- D
Xét hệ gồm hai xe lăn, thời gian tương tác là ngắn nên có thể coi là hệ kín.
Trước khi đốt dây, hai xe nằm yên nên: $ \overrightarrow p =\overrightarrow 0 . $
Sau khi đốt dây: $ \overrightarrow{p'}={ m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }} $
Áp dụng định luật bảo toàn động lượng, ta có: $ \overrightarrow{p'}=\overrightarrow p \Rightarrow { m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }}=0\Rightarrow \dfrac{\overrightarrow{{ v _ 2 }}}{\overrightarrow{{ v _ 1 }}}=-\dfrac{{ m _ 1 }}{{ m _ 2 }} $
Câu 12: Trong các hiện tượng sau, đâu là va chạm mềm?
- A
- B
- C
- D
Theo định nghĩa, va chạm mềm: sau va chạm, hai vật dính vào nhau rồi chuyển động với cùng vận tốc.
Câu 13: Một vật khối lượng $ { m _ 1 } $ chuyển động trên một mặt phẳng nằm ngang nhẵn với vận tốc $ \overrightarrow{{ v _ 1 }} $ , đến va chạm với một vật khối lượng $ { m _ 2 } $ đang nằm yên trên mặt phẳng nằm ngang ấy. Biết rằng sau va chạm hai vật nhập làm một, chuyển động cùng vận tốc $ \overrightarrow v $ là:
- A
- B
- C
- D
SGK Vật lí 10, trang 125, mục 3. Va chạm mềm: $ \overrightarrow v =\dfrac{{ m _ 1 }\overrightarrow{{ v _ 1 }}}{{ m _ 1 }+{ m _ 2 }} $
Câu 14: Hiện tượng nào sau đây là va chạm đàn hồi?
- A
- B
- C
- D
Hiện tượng hai viên bi chuyển động ngược chiều rồi nảy lại thỏa mãn điều kiện của va chạm đàn hồi.
Câu 15:  Hai xe lăn được nối với nhau bằng một sợi dây để ép chặt một lò xo đặt giữa hai xe (như hình vẽ). Thoạt đầu cả hai xe nằm yên trên mặt đất. Khi đốt dây, lò xo bung ra, đẩy hai xe chuyển động theo hai hướng ngược nhau. Xe 1 có khối lượng m1 = 100g chuyển động với tốc độ 6 m/s. Hỏi xe 2 có khối lượng m2 = 300g chuyển động với tốc độ là bao nhiêu?
Hai xe lăn được nối với nhau bằng một sợi dây để ép chặt một lò xo đặt giữa hai xe (như hình vẽ). Thoạt đầu cả hai xe nằm yên trên mặt đất. Khi đốt dây, lò xo bung ra, đẩy hai xe chuyển động theo hai hướng ngược nhau. Xe 1 có khối lượng m1 = 100g chuyển động với tốc độ 6 m/s. Hỏi xe 2 có khối lượng m2 = 300g chuyển động với tốc độ là bao nhiêu?
 Hai xe lăn được nối với nhau bằng một sợi dây để ép chặt một lò xo đặt giữa hai xe (như hình vẽ). Thoạt đầu cả hai xe nằm yên trên mặt đất. Khi đốt dây, lò xo bung ra, đẩy hai xe chuyển động theo hai hướng ngược nhau. Xe 1 có khối lượng m1 = 100g chuyển động với tốc độ 6 m/s. Hỏi xe 2 có khối lượng m2 = 300g chuyển động với tốc độ là bao nhiêu?
Hai xe lăn được nối với nhau bằng một sợi dây để ép chặt một lò xo đặt giữa hai xe (như hình vẽ). Thoạt đầu cả hai xe nằm yên trên mặt đất. Khi đốt dây, lò xo bung ra, đẩy hai xe chuyển động theo hai hướng ngược nhau. Xe 1 có khối lượng m1 = 100g chuyển động với tốc độ 6 m/s. Hỏi xe 2 có khối lượng m2 = 300g chuyển động với tốc độ là bao nhiêu?- A
- B
- C
- D
Xét hệ gồm hai xe lăn, thời gian tương tác là ngắn nên có thể coi là hệ kín.
Trước khi đốt dây, hai xe nằm yên nên: $ \overrightarrow p =\overrightarrow 0 . $
Sau khi đốt dây: $ \overrightarrow{p'}={ m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }} $
Áp dụng định luật bảo toàn động lượng, ta có: $ \overrightarrow{p'}=\overrightarrow p \Rightarrow { m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }}=0\Rightarrow \overrightarrow{{ v _ 2 }}=-\dfrac{{ m _ 1 }}{{ m _ 2 }}\overrightarrow{{ v _ 1 }} $
Tốc độ của xe 2 là: $ { v _ 2 }=\dfrac{{ m _ 1 }}{{ m _ 2 }}{ v _ 1 }=\dfrac{100}{300}.6=2\left( m/s \right) $
Câu 16: Vật m1 chuyển động với vận tốc v1 tới va chạm hoàn toàn đàn hồi với vật m2 đang đứng yên. Động lượng của hệ sau khi va chạm là?
- A
- B
- C
- D
Động lượng lúc đầu của hệ là: $ \overrightarrow p ={ m _ 1 }\overrightarrow{{ v _ 1 }} $
Do động lượng được bảo toàn nên động lượng lúc sau cũng bằng như vậy.
Câu 17: Một xe chở cát có khối lượng $ { m _ 1 }=390kg $ đang chuyển động theo phương ngang với vận tốc $ { v _ 1 }=8m/s $ , thì một hòn đá có khối lượng $ { m _ 2 }=10kg $ bay theo phương hợp với phương ngang 1 góc $ {{60}^ 0 } $ cùng chiều với vận tốc $ { v _ 2 }=12m/s $ đến cắm vào xe cát. Vận tốc của xe sau khi hòn đá rơi vào là:
- A
- B
- C
- D

Xét hệ gồm xe và hòn đá là hệ kín.
Chọn chiều dương là chiều chuyển động của xe.
Động lượng của hệ trước va chạm là: $ \overrightarrow p ={ m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }} $
Động lượng của hệ sau va chạm là: $ \overrightarrow p '=({ m _ 1 }+{ m _ 2 })\overrightarrow{v'} $
Định luật bảo toàn động lượng: $ \overrightarrow p =\overrightarrow p '\Leftrightarrow { m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }}=({ m _ 1 }+{ m _ 2 })\overrightarrow v '\quad \left( * \right) $
Chiếu (*) lên phương chuyển động nằm ngang:
$ \begin{array}{l} & { m _ 1 }{ v _ 1 }+{ m _ 2 }.{ v _ 2 }.\cos {{60}^ 0 }=({ m _ 1 }+{ m _ 2 })v' \\ & \Rightarrow v'=\dfrac{{ m _ 1 }{ v _ 1 }+{ m _ 2 }.{ v _ 2 }.c\text{os}{{60}^ 0 }}{{ m _ 1 }+{ m _ 2 }}=\dfrac{390.8+10.12.c\text{os}{{60}^ 0 }}{390+10}=7,95m/s \\ \end{array} $
Câu 18: Vật 1 có m1, v1 chuyển động ngược chiều với vật 2 có m2, v2 (v1 > v2). Hai vật va chạm hoàn toàn đàn hồi và cùng bật ngược lại với vận tốc v1’ và v2’. Khẳng định nào sau đây là đúng?
- A
- B
- C
- D
Áp dụng định luật bảo toàn động lượng: $ { m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }}={ m _ 1 }\overrightarrow{{ v _ 1 }'}+{ m _ 2 }\overrightarrow{{ v _ 2 }'} $
Giá trị của v1’ và v2’ phụ thuộc vào m1 và m2 nên chưa xác định được.
Câu 19: Một chiếc xe đang chạy trên đường ngang có động lượng là 20 kgm/s va chạm vào một chiếc xe khác đang đứng yên. Biết va chạm là va chạm mềm, sau va chạm động lượng của hai xe là:
- A
- B
- C
- D
$ { p _ 1 }=20kg.m/s;{ p _ 2 }=0. $
Tổng động lượng của hệ 2 xe trước khi va chạm là: $ p={ p _ 1 }+{ p _ 2 }=20kg.m/s $
Coi hệ là kín, áp dụng định luật bảo toàn động lượng ta có:
$ p=p\Leftrightarrow p'=20kg.m/s $
Câu 20: Hai xe lăn nhỏ có khối lượng $ { m _ 1 }=300g $ và $ { m _ 2 }=2kg $ chuyển động trên mặt phẳng nằm ngang với tốc độ tương ứng $ { v _ 1 }=2m/s $ và $ { v _ 2 }=0,8m/s $ theo hướng hợp với nhau một góc $ {{45}^ 0 } $ . Sau khi va chạm hai xe dính vào nhau và chuyển động cùng vận tốc. Bỏ qua sức cản. Tốc độ của hai xe sau va chạm là
- A
- B
- C
- D
+ Trước va chạm:
- Động lượng xe 1 là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=0,3.2=0,6\left( kg.m/s \right). $
- Động lượng của xe 2 là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=2.0,8=1,6\left( kg.m/s \right) $
- Tổng động lượng của hệ trước va chạm là: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
+ Sau khi va chạm hai xe dính vào nhau và chuyển động cùng vận tốc v, ta có:
$ p'=\left( { m _ 1 }+{ m _ 2 } \right)v=\left( 0,3+2 \right).v=2,3v\left( kg.m/s \right) $
Áp dụng định luật bảo toàn động lượng, ta có: $ \overrightarrow p =\overrightarrow p '\Leftrightarrow \overrightarrow p '=\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
$ \begin{array}{l} & \left( \widehat{\overrightarrow{{ p _ 1 }};\overrightarrow{{ p _ 2 }}} \right)={{45}^ 0 } \\ & \Rightarrow p'=\sqrt{{{\left( { p _ 1 } \right)}^ 2 }+{{\left( { p _ 2 } \right)}^ 2 }+2{ p _ 1 }.{ p _ 2 }.c\text{os}{{45}^ 0 }} \\ & \Rightarrow 2,3v=\sqrt{{{\left( 0,6 \right)}^ 2 }+{{\left( 1,6 \right)}^ 2 }+2.0,6.1,6.c\text{os}{{45}^ 0 }} \\ & \Rightarrow v=0,9\left( m/s \right) \\ \end{array} $
Câu 21: Một chiếc xe chạy trên đường ngang với vận tốc 10m/s va chạm vào một chiếc xe khác đang đứng yên và có cùng khối lượng. Biết va chạm là va chạm mềm, sau va chạm tốc độ của hai xe là:
- A
- B
- C
- D
$ { m _ 1 }={ m _ 2 }=m;{ v _ 1 }=10m/s;{ v _ 2 }=0. $
Tổng động lượng của hệ 2 xe trước khi va chạm là:
p = m1v1 + m2v2 = m1v1 = 10m
Va chạm là va chạm mềm, sau va chạm hai vật chuyển động cùng vận tốc nên tổng động lượng của hệ sau va chạm là: $ p=\left( { m _ 1 }+{ m _ 2 } \right)v=2mv $
Áp dụng định luật bảo toàn động lượng ta có:
$ p=p\Leftrightarrow 10m=2mv\Rightarrow v=5(m/s) $
Câu 22: Những đại lượng không được bảo toàn trong va chạm mềm là:
- A
- B
- C
- D
Trong va chạm mềm, chỉ có động lượng được bảo toàn.
Câu 23: Một xe chở cát có khối lượng $ { m _ 1 }=390kg $ đang chuyển động theo phương ngang với vận tốc $ { v _ 1 }=8m/s $ , thì một hòn đá có khối lượng $ { m _ 2 }=10kg $ rơi thẳng đứng với vận tốc $ { v _ 2 }=12m/s $ xuống cắm vào xe cát. Vận tốc của xe sau khi hòn đá rơi vào là:
- A
- B
- C
- D
Xét hệ gồm xe và hòn đá là hệ kín.
Chọn chiều dương là chiều chuyển động của xe.
Động lượng của hệ trước va chạm là: $ \overrightarrow p ={ m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }} $
Động lượng của hệ sau va chạm là: $ \overrightarrow p '=({ m _ 1 }+{ m _ 2 })\overrightarrow{v'} $
Định luật bảo toàn động lượng: $ \overrightarrow p =\overrightarrow p '\Leftrightarrow { m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }}=({ m _ 1 }+{ m _ 2 })\overrightarrow v '\quad \left( * \right) $
Chiếu (*) lên phương chuyển động nằm ngang:
$ \begin{array}{l} & { m _ 1 }{ v _ 1 }+{ m _ 2 }.0=({ m _ 1 }+{ m _ 2 })v' \\ & \Rightarrow v'=\dfrac{{ m _ 1 }{ v _ 1 }}{{ m _ 1 }+{ m _ 2 }}=\dfrac{390.8}{390+10}=7,8m/s \\ \end{array} $
Câu 24: Hai xe nhỏ khối lượng như nhau đặt trên mặt bàn (hình vẽ). Một sợi dây mảnh luồn qua một lò xo để nối hai xe ép chặt lò xo. Hai đầu lò xo tì lên thành của hai xe. Người ta đốt cháy sợi dây. Hai xe sẽ chuyển động như thế nào?


- A
- B
- C
- D
Xét hệ gồm hai xe lăn ( $ { m _ 1 }={ m _ 2 }=m $ ), thời gian tương tác là ngắn nên có thể coi là hệ kín.
Trước khi đốt dây, hai xe nằm yên nên động lượng của hệ bằng 0: p = 0
Sau khi đốt dây : $ p'=mv+mv' $
Áp dụng định luật bảo toàn động lượng, ta có: $ p'=0\Rightarrow mv+mv'=0\Rightarrow v=-v' $
Câu 25: Trong va chạm đàn hồi, đại lượng vật lí nào được bảo toàn?
- A
- B
- C
- D
Trong va chạm đàn hồi, động lượng và động năng của hệ vật được bảo toàn.
Câu 26: Hai viên bi A và B chuyển động ngược chiều rồi va chạm đàn hồi xuyên tâm với nhau. Động lượng của hệ sau va chạm là?
- A
- B
- C
- D
Động lượng lúc đầu của hệ là: $ \overrightarrow p ={ m _ A }\overrightarrow{{ v _ A }}+{ m _ B }\overrightarrow{{ v _ B }} $
Do động lượng được bảo toàn nên động lượng lúc sau cũng bằng động lượng lúc đầu.
Câu 27: Trong các hiện tượng sau, hiện tượng nào không phải là va chạm mềm?
- A
- B
- C
- D
Hiện tượng quả bóng đập vào tường rồi nảy lại có sự biến thiên động lượng nên không phải va chạm mềm.
Câu 28: Một vật khối lượng $ { m _ 1 } $ chuyển động trên một mặt phẳng nằm ngang nhẵn với vận tốc $ \overrightarrow{{ v _ 1 }} $ , đến va chạm với một vật khối lượng $ { m _ 2 } $ đang nằm yên trên mặt phẳng nằm ngang ấy. Biết rằng sau va chạm hai vật nhập làm một, chuyển động cùng vận tốc $ \overrightarrow v $ . Biểu thức của định luật bảo toàn động lượng là
- A
- B
- C
- D
SGK Vật lí 10, trang 125, mục 3. Va chạm mềm: $ \overrightarrow v =\dfrac{{ m _ 1 }\overrightarrow{{ v _ 1 }}}{{ m _ 1 }+{ m _ 2 }} $.
Câu 29: Một xe chở cát có khối lượng $ { m _ 1 }=390kg $ đang chuyển động theo phương ngang với vận tốc $ { v _ 1 }=8m/s $ , thì một hòn đá có khối lượng $ { m _ 2 }=10kg $ bay ngang ngược chiều với vận tốc $ { v _ 2 }=12m/s $ đến cắm vào xe cát. Vận tốc của xe sau khi hòn đá rơi vào là:
- A
- B
- C
- D
Xét hệ gồm xe và hòn đá là hệ kín.
Chọn chiều dương là chiều chuyển động của xe.
Động lượng của hệ trước va chạm là: $ \overrightarrow p ={ m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }} $
Động lượng của hệ sau va chạm là: $ \overrightarrow p '=({ m _ 1 }+{ m _ 2 })\overrightarrow{v'} $
Định luật bảo toàn động lượng: $ \overrightarrow p =\overrightarrow p '\Leftrightarrow { m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }}=({ m _ 1 }+{ m _ 2 })\overrightarrow v '\quad \left( * \right) $
Chiếu (*) lên phương chuyển động nằm ngang:
$ \begin{array}{l} & { m _ 1 }{ v _ 1 }-{ m _ 2 }{ v _ 2 }=({ m _ 1 }+{ m _ 2 })v' \\ & \Rightarrow v'=\dfrac{{ m _ 1 }{ v _ 1 }-{ m _ 2 }{ v _ 2 }}{{ m _ 1 }+{ m _ 2 }}=\dfrac{390.8-10.12}{390+10}=7,5m/s \\ \end{array} $
Câu 30: Một xe chở cát có khối lượng $ { m _ 1 }=390kg $ đang chuyển động theo phương ngang với vận tốc $ { v _ 1 }=8m/s $ , thì một hòn đá có khối lượng $ { m _ 2 }=10kg $ bay ngang cùng chiều với vận tốc $ { v _ 2 }=12m/s $ đến cắm vào xe cát. Vận tốc của xe sau khi hòn đá rơi vào là:
- A
- B
- C
- D
Xét hệ gồm xe và hòn đá là hệ kín.
Chọn chiều dương là chiều chuyển động của xe.
Động lượng của hệ trước va chạm là: $ \overrightarrow p ={ m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }} $
Động lượng của hệ sau va chạm là: $ \overrightarrow p '=({ m _ 1 }+{ m _ 2 })\overrightarrow{v'} $
Định luật bảo toàn động lượng: $ \overrightarrow p =\overrightarrow p '\Leftrightarrow { m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }}=({ m _ 1 }+{ m _ 2 })\overrightarrow v '\quad \left( * \right) $
Chiếu (*) lên phương chuyển động nằm ngang:
$ \begin{array}{l} & { m _ 1 }{ v _ 1 }+{ m _ 2 }{ v _ 2 }=({ m _ 1 }+{ m _ 2 })v' \\ & \Rightarrow v'=\dfrac{{ m _ 1 }{ v _ 1 }+{ m _ 2 }{ v _ 2 }}{{ m _ 1 }+{ m _ 2 }}=\dfrac{390.8+10.12}{390+10}=8,1m/s \\ \end{array} $
Câu 31: Một đầu máy xe lửa có khối lượng 100 tấn chuyển động thẳng đều theo phương ngang với vận tốc $ { v _ 1 }=1,5m/s $ để ghép vào một đoàn tàu gồm 10 toa, mỗi toa có khối lượng m đang đứng yên trên đường ray. Giả sử sau va chạm đầu tàu được gắn với các toa, bỏ qua mọi ma sát. Sau va chạm, vận tốc của đoàn tàu là 0,5 m/s. Giá trị m là:
- A
- B
- C
- D
Xét hệ gồm đầu máy xe lửa (m1) và các toa tàu (m2). Hệ là kín.
m1 = 100 tấn = 105 kg. m2 = 10.m.
Chọn chiều dương là chiều chuyển động của đầu toa tàu trước lúc va chạm.
Áp dụng định luật bảo toàn động lượng cho hệ tàu có:
$ \begin{array}{l} & { m _ 1 }{ v _ 1 }=\left( { m _ 1 }+{ m _ 2 } \right).{ v _ 2 }\Leftrightarrow { m _ 1 }{ v _ 1 }=\left( { m _ 1 }+10m \right).{ v _ 2 } \\ & m=\dfrac{{ m _ 1 }{ v _ 1 }-{ m _ 1 }{ v _ 2 }}{10{ v _ 2 }}=\dfrac{{{10}^ 5 }.1,5-{{10}^ 5 }.0,5}{10.0,5}=20000\left( kg \right) \\ \end{array} $
Câu 32: Vật 1 chuyển động với vận tốc v đến va chạm mềm với vật 2 đang đứng yên rồi cả hai chuyển động với vận tốc V. Điều nào sau đây là đúng?
- A
- B
- C
- D
Áp dụng định luật bảo toàn động lượng: $ \overrightarrow V =\dfrac{{ m _ 1 }\overrightarrow v }{{ m _ 1 }+{ m _ 2 }} $
Do khối lượng luôn dương nên $ \overrightarrow v \uparrow \uparrow \overrightarrow V $
Câu 33: Một người khối lượng m1 = 50kg đang chạy với vận tốc v1 = 4m/s thì nhảy lên một chiếc xe khối lượng m2 = 80kg chạy song song ngang với người này với vận tốc v2 = 3m/s. Sau đó, xe và người vẫn tiếp tục chuyển động theo phương cũ. Nếu ban đầu xe và người chuyển động ngược chiều thì vận tốc xe sau khi người này nhảy lên là
- A
- B
- C
- D
Xét hệ: Xe + người là hệ kín.
Chọn chiều dương là chiều chuyển động của xe.
Theo định luật BT động lượng: $ { m _ 1 }.{{\overrightarrow v }_ 1 }+{ m _ 2 }.{{\overrightarrow v }_ 2 }=\left( { m _ 1 }+{ m _ 2 } \right)\overrightarrow v $
Khi người nhảy ngược chiều thì $ v=\dfrac{-{ m _ 1 }{ v _ 1 }+{ m _ 2 }{ v _ 2 }}{{ m _ 1 }+{ m _ 2 }}=\dfrac{-50.4+80.3}{50+80}=0,3m/s $
Vậy xe tiếp tục chuyển động theo hướng cũ với vận tốc 0,3 m/s.
Câu 34:  Hai xe lăn được nối với nhau bằng một sợi dây để ép chặt một lò xo đặt giữa hai xe (như hình vẽ). Thoạt đầu cả hai xe nằm yên trên mặt đất. Khi đốt dây, lò xo bung ra, đẩy hai xe chuyển động theo hai hướng ngược nhau. Xe 1 có khối lượng m1 = 100g chuyển động được 18m thì dừng lại. Hỏi tốc độ của xe 2 có khối lượng m2 = 300g ngay sau khi đốt dây bằng bao nhiêu? Biết hệ số ma sát trượt giữa xe và mặt đất là $ {{\mu }_ t }=0,5 $ .
Hai xe lăn được nối với nhau bằng một sợi dây để ép chặt một lò xo đặt giữa hai xe (như hình vẽ). Thoạt đầu cả hai xe nằm yên trên mặt đất. Khi đốt dây, lò xo bung ra, đẩy hai xe chuyển động theo hai hướng ngược nhau. Xe 1 có khối lượng m1 = 100g chuyển động được 18m thì dừng lại. Hỏi tốc độ của xe 2 có khối lượng m2 = 300g ngay sau khi đốt dây bằng bao nhiêu? Biết hệ số ma sát trượt giữa xe và mặt đất là $ {{\mu }_ t }=0,5 $ .
 Hai xe lăn được nối với nhau bằng một sợi dây để ép chặt một lò xo đặt giữa hai xe (như hình vẽ). Thoạt đầu cả hai xe nằm yên trên mặt đất. Khi đốt dây, lò xo bung ra, đẩy hai xe chuyển động theo hai hướng ngược nhau. Xe 1 có khối lượng m1 = 100g chuyển động được 18m thì dừng lại. Hỏi tốc độ của xe 2 có khối lượng m2 = 300g ngay sau khi đốt dây bằng bao nhiêu? Biết hệ số ma sát trượt giữa xe và mặt đất là $ {{\mu }_ t }=0,5 $ .
Hai xe lăn được nối với nhau bằng một sợi dây để ép chặt một lò xo đặt giữa hai xe (như hình vẽ). Thoạt đầu cả hai xe nằm yên trên mặt đất. Khi đốt dây, lò xo bung ra, đẩy hai xe chuyển động theo hai hướng ngược nhau. Xe 1 có khối lượng m1 = 100g chuyển động được 18m thì dừng lại. Hỏi tốc độ của xe 2 có khối lượng m2 = 300g ngay sau khi đốt dây bằng bao nhiêu? Biết hệ số ma sát trượt giữa xe và mặt đất là $ {{\mu }_ t }=0,5 $ .- A
- B
- C
- D
Xét hệ gồm hai xe lăn, thời gian tương tác là ngắn nên có thể coi là hệ kín.
Trước khi đốt dây, hai xe nằm yên nên: $ \overrightarrow p =\overrightarrow 0 . $
Sau khi đốt dây: $ \overrightarrow{p'}={ m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }} $
Áp dụng định luật bảo toàn động lượng, ta có: $ \overrightarrow{p'}=\overrightarrow p \Rightarrow { m _ 1 }\overrightarrow{{ v _ 1 }}+{ m _ 2 }\overrightarrow{{ v _ 2 }}=0\Rightarrow \overrightarrow{{ v _ 2 }}=-\dfrac{{ m _ 1 }}{{ m _ 2 }}\overrightarrow{{ v _ 1 }} $
Tỉ số tốc độ của hai xe: $ \dfrac{{ v _ 2 }}{{ v _ 1 }}=\dfrac{{ m _ 1 }}{{ m _ 2 }}=\dfrac{100}{300}=\dfrac{1}{3} $
+ Sau khi đốt dây, vật m1 chuyển động chậm dần dưới tác dụng của lực ma sát.
Theo định luật II Niutơn, gia tốc của chuyển động là:
$ a=\dfrac{{- F _{m\text s }}} m =\dfrac{-\mu mg} m =-\mu g=-0,5.10=-5\left( m/{ s ^ 2 } \right) $
Áp dụng công thức: $ { v ^ 2 }-v_ 0 ^ 2 =2\text{as}\Rightarrow 0-v_ 1 ^ 2 =2.\text (-5) \text{.18}\Rightarrow {{\text v }_ 1 }=6\sqrt{5} \left( m/s \right) $
Tốc độ của vật 2 sau khi đốt dây là: $ { v _ 2 }=\dfrac{1}{3} { v _ 1 }=\dfrac{1}{3} .6\sqrt{5} =2\sqrt{5} \left( m/s \right) $
Câu 35: Hai vật chuyển động ngược chiều va chạm hoàn toàn đàn hồi. Sau va chạm, hai vật chuyển động như thế nào?
- A
- B
- C
- D
Hai vật có thể chuyển động theo cả 3 trường hợp trên, tùy thuộc vào động lượng của hệ lúc đầu và lúc sau.
Câu 36: Một quả đạn pháo có động lượng $ \overrightarrow p $ bị vỡ thành hai mảnh với các động lượng lần lượt là $ \overrightarrow{{ p _ 1 }} $ và $ \overrightarrow{{ p _ 2 }} $ . Điều nào sau đây là đúng?
- A
- B
- C
- D
Do nội lực rất lớn so với ngoại lực nên hệ được coi là hệ kín, động lượng của hệ được bảo toàn: $ \overrightarrow p =\overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }} $
Câu 37: Va chạm đàn hồi xuyên tâm là gì?
- A
- B
- C
- D
Va chạm đàn hồi xuyên tâm là va chạm xảy ra giữa các vật có cùng phương chuyển động và trọng tâm của vật nằm trên phương chuyển động.
Câu 38: Vật 1 chuyển động với vận tốc v đến va chạm hoàn toàn đàn hồi với vật 2 đang đứng yên. Sau va chạm, trường hợp nào không thể xảy ra?
- A
- B
- C
- D
Áp dụng định luật bảo toàn động lượng: $ { m _ 1 }\overrightarrow v =({ m _ 1 }+{ m _ 2 })\overrightarrow{v'} $
Sau va chạm, hai vật không thể chuyển động ngược chiều vật 1.
Câu 39: Một xe ôtô có khối lượng $ { m _ 1 } $ = 3 tấn chuyển động thẳng với vận tốc \[{v_1}\] = 1,5m/s đến va chạm mềm với một xe gắn máy đang đứng yên có khối lượng \[{m_2}\] = 100kg. Vận tốc các xe sau va chạm là:
- A
- B
- C
- D
Xem hệ hai xe là hệ cô lập
Áp dụng địmh luật bảo toàn động lượng của hệ: $ { m _ 1 }.{{\vec v }_ 1 }=({ m _ 1 }+{ m _ 2 })\vec v $
$ \vec v $ cùng hướng với vận tốc $ {{\vec v }_ 1 } $ .
- Vận tốc của mỗi xe là: $ v=\dfrac{{ m _ 1 }.{ v _ 1 }}{{ m _ 1 }+{ m _ 2 }}=\dfrac{3000.1,5}{3000+100}=\text 1,45\left( m/s \right) $
Câu 40: Một đầu máy xe lửa có khối lượng 100 tấn chuyển động thẳng đều theo phương ngang với vận tốc $ { v _ 1 }=1,5m/s $ để ghép vào một đoàn tàu gồm 10 toa, mỗi toa 20 tấn đang đứng yên trên đường ray. Giả sử sau va chạm đầu tàu được gắn với các toa, bỏ qua mọi ma sát. Sau va chạm, vận tốc của đoàn tàu có giá trị là:
- A
- B
- C
- D
Xét hệ gồm đầu máy xe lửa (m1) và các toa tàu (m2). Hệ là kín.
m1 = 100 tấn = 105 kg. m2 = 10.20 tấn = 200 tấn = 2.105 kg.
Chọn chiều dương là chiều chuyển động của đầu toa tàu trước lúc va chạm.
Áp dụng định luật bảo toàn động lượng cho hệ tàu có:
$ \begin{array}{l} & { m _ 1 }{ v _ 1 }=\left( { m _ 1 }+{ m _ 2 } \right).{ v _ 2 } \\ & \Rightarrow { v _ 2 }=\dfrac{{ m _ 1 }{ v _ 1 }}{{ m _ 1 }+{ m _ 2 }}=\dfrac{{{10}^ 5 }.1,5}{\left( {{10}^ 5 }+{{2.10}^ 5 } \right)}=0,5\left( m/s \right) \\ \end{array} $
Câu 41: Vật 1 chuyển động với vận tốc v đến va chạm mềm với vật 2 đang đứng yên rồi cả hai chuyển động với vận tốc V. Điều nào sau đây là đúng?
- A
- B
- C
- D
Áp dụng định luật bảo toàn động lượng: $ \overrightarrow V =\dfrac{{ m _ 1 }\overrightarrow v }{{ m _ 1 }+{ m _ 2 }} $
Do (m1 + m2) > m1, nên v > V
Câu 42: Một chiếc xe đang chạy trên đường ngang có động lượng là 30 kgm/s va chạm vào một chiếc xe khác đang đang chuyển động vuông góc với động lượng là 40 kg.m/s. Sau va chạm, hai xe dính vào nhau và cùng chuyển động. Động lượng của 2 xe sau va chạm là:
- A
- B
- C
- D
Ta có: $ { p _ 1 }=30kg.m/s;{ p _ 2 }=40kg.m/s $
Coi hệ là kín. Áp dụng định luật bảo toàn động lượng ta có: $ \overrightarrow{{ p _ 1 }}+\overrightarrow{{ p _ 2 }}=\overrightarrow p $
$ \overrightarrow{{ p _ 1 }}\bot \overrightarrow{{ p _ 2 }}\Rightarrow p=\sqrt{{{\left( { p _ 1 } \right)}^ 2 }+{{\left( { p _ 2 } \right)}^ 2 }}=\sqrt{{{\left( 30 \right)}^ 2 }+{{\left( 40 \right)}^ 2 }}=50\left( kg.m/s \right) $
Câu 43: Viên bi A có khối lượng $ { m _ 1 }=60g $ đang chuyển động với tốc độ 5m/s trên mặt phẳng nằm ngang tới va chạm vào viên bi B có khối lượng $ { m _ 2 } $ chuyển động ngược chiều với tốc độ 7,5 m/s. Sau va chạm, hai viên bi đứng yên. Khối lượng $ { m _ 2 } $ là:
- A
- B
- C
- D
Chọn chiều dương là chiều chuyển động của viên bi A.
+ Trước va chạm:
- Động lượng của bi A là: $ { p _ 1 }={ m _ 1 }{ v _ 1 }=0,06.5=0,3\left( kg.m/s \right). $
- Động lượng của viên bi B là: $ { p _ 2 }={ m _ 2 }{ v _ 2 }=-7,5{ m _ 2 } $
- Tổng động lượng của hệ trước va chạm là: $ p={ p _ 1 }+{ p _ 2 }=0,3-7,5{ m _ 2 } $
+ Sau va chạm hai viên bi đứng yên nên tổng động lượng của hệ bằng 0: p’ = 0.
Áp dụng định luật bảo toàn động lượng, ta có: p = p’
$ \Leftrightarrow 0,3-7,5{ m _ 2 }=0\Rightarrow { m _ 2 }=\dfrac{0,3}{7,5}=0,04(kg)=40\left( g \right) $
Câu 44: Va chạm nào sau đây là va chạm mềm?
- A
- B
- C
- D
SGK Vật lí 10, trang 125, mục 3. Va chạm mềm: sau va chạm, hai vật gắn vào nhau và chuyển động với cùng vận tốc
Xem thêm các bài tiếp theo bên dưới