Xét các khẳng định sau i. Nếu giá trị nhỏ nhất của hàm đa thức bậc bốn

Xét các khẳng định sau
i. Nếu giá trị nhỏ nhất của hàm đa thức bậc bốn $\Large y=f(x)$ trên $\Large \mathbb{R}$ bằng $\Large m$ thì có số thực $\Large x_1$ thỏa mãn $\Large f(x_1)=m$, $\Large f(x) > m\ \forall x\in (-\infty; +\infty)\setminus \begin{Bmatrix} x_1 \end{Bmatrix}$.

ii. Nếu giá trị nhỏ nhất của hàm đa thức bậc bốn $\Large y=f(x)$ trên $\Large \mathbb{R}$ bằng $\Large m$ thì có số thực $\Large x_1$ thỏa mãn $\Large f(x_1)=m$, $\Large f(x) \geq m\ \forall x\in (-\infty; +\infty)\setminus \begin{Bmatrix} x_1 \end{Bmatrix}$.

iii. Nếu giá trị lớn nhất của hàm đa thức bậc bốn $\Large y=f(x)$ trên $\Large \mathbb{R}$ bằng $\Large m$ thì có số thực $\Large x_1$ thỏa mãn $\Large f(x_1)=m$, $\Large f(x) < m\ \forall x\in (-\infty; +\infty)\setminus \begin{Bmatrix} x_1 \end{Bmatrix}$.

iv. Nếu giá trị lớn nhất của hàm đa thức bậc bốn $\Large y=f(x)$ trên $\Large \mathbb{R}$ bằng $\Large m$ thì có số thực $\Large x_1$ thỏa mãn $\Large f(x_1)=m$, $\Large f(x) \leq m\ \forall x\in (-\infty; +\infty)\setminus \begin{Bmatrix} x_1 \end{Bmatrix}$.

Số khẳng định đúng trong các khẳng định trên là

• A. 4.
• B. 3.
• C. 1.
• D. 2.

+) Dễ thấy khẳng định ii, iv là đúng.
+) Xét hàm số $\Large y=x^4-2x^2$ có bảng biến thiên như sau:

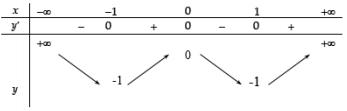
Dựa vào bảng biến thiên ta thấy giá trị nhỏ nhất của $\Large y=f(x)$ trên $\Large \mathbb{R}$ là $\Large m=-1$ tại $\Large x_1=-1$ và $\Large f(1)=-1$ nhưng khẳng định $\Large f(x) > -1\ \forall x\in (-\infty; +\infty)\setminus \begin{Bmatrix} -1 \end{Bmatrix}$ là khẳng định sai.

Do đó khẳng định i sai.

+) Xét hàm số $\Large y=-x^4+2x$ có bảng biến thiên như sau:

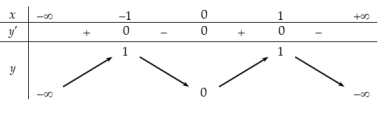
Dựa vào bảng biến thiên ta thấy giá trị lớn nhất của $\Large y=f(x)$ trên $\Large \mathbb{R}$ là $\Large m=1$ tại $\Large x_1=-1$ và $\Large f(1)=1$ nhưng khẳng định $\Large f(x) < 1\ \forall x\in (-\infty; +\infty)\setminus \begin{Bmatrix} -1 \end{Bmatrix}$ là khẳng định sai.

Do đó khẳng định iii là sai.
Vậy số khẳng định đúng trong các khẳng định trên là: 2.