Với mọi giá trị $\Large m \geq a\sqrt{b}$ với $\Large a, b \in \mathbb

Với mọi giá trị $\Large  m \geq a\sqrt{b}$ với $\Large  a, b \in \mathbb{R}$ thì hàm số $\Large  y = 2x^{3} - mx^{2} + 2x + 5$ đồng biến trên khoảng (-2; 0). Khi đó a-b bằng?

• A. A. -2
• B. B. 1
• C. C. -5
• D. D. 3

Ta có $\Large  y = 2x^{3} - mx^{2} + 2x + 5$ có $\Large y' = 6x^{2} - 2mx + 2$

Hàm số $\Large  y = 2x^{3} - mx^{2} + 2x + 5$ đồng biến trên khoảng (-2; 0) khi và chỉ khi $\Large  y' \geq 0, \forall x \in (-2; 0) \Leftrightarrow 6x^{2} - 2mx + 2 \geq 0, \forall x \in (-2; 0)$

$\Large  \Leftrightarrow 2mx \leq 6x^{2} + 2, \forall x \in (-2; 0) \Leftrightarrow m \geq \dfrac{6x^{2} + 2}{2x}, \forall x \in (-2; 0).$

Xét hàm số $\Large  g(x) = \dfrac{6x^{2}+2}{2x} = 3x + \dfrac{1}{x}$ với $\Large  x \in (-2; 0)$

Có $\Large  g'(x) = 3 - \dfrac{1}{x^{2}} \Rightarrow g'(x) = 0 \Leftrightarrow 3 - \dfrac{1}{x^{2}} = 0 \Leftrightarrow x^{2} = \dfrac{1}{3} \Leftrightarrow x = \pm \dfrac{\sqrt{3}}{3}$

Bảng biến thiên:

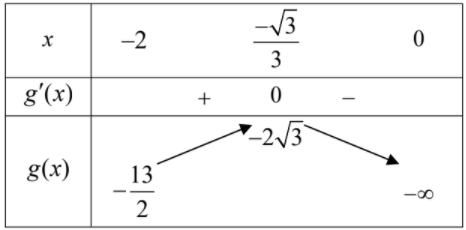
Từ bảng biến thiên suy ra $\Large m \geq -2\sqrt{3}$ nên a = -2; b = 3. Do đó a - b = -2 - 3 = -5