Cho hình trụ có đáy là hai đường tròn tâm O và O', bán kính đáy bằng c

Cho hình trụ có đáy là hai đường tròn tâm O và O', bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy có tâm O lấy điểm A, trên đường tròn tâm O' lấy điểm B. Đặt $\Large \alpha$ là góc giữa AB và đáy. Biết rằng thể tích khối tứ diện OO'AB đạt giá trị lớn nhất. Khẳng định nào sau đây đúng? 

• A. A. $\Large \tan \alpha = \sqrt{2}$
• B. B. $\Large \tan\alpha = \dfrac{1}{2}$
• C. C. $\Large \tan \alpha = 1$
• D. D. $\Large \tan \alpha = \dfrac{1}{\sqrt{2}}$

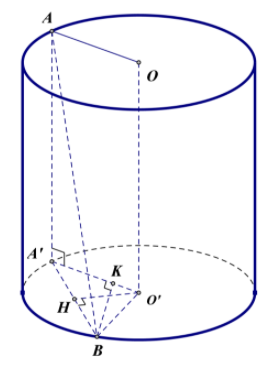
Ta có $\Large V_{OAO'B} = V_{B.OAO'} = \dfrac{1}{3}d.(B,(OAO')).S_{OAO'}$

Mà $\Large S_{OAO'} = \dfrac{1}{2}.OO'.OA = \dfrac{1}{2}.2a.2a = 2a^{2}$

Kẻ AA' vuông góc với mặt phẳng chứa đường tròn (O') tại A' $\Large \Rightarrow \widehat{ABA'} = \alpha$. Suy ra $\Large \tan \alpha = \dfrac{AA'}{A'B} \Rightarrow A'B = \dfrac{2a}{\tan \alpha}$

Kẻ $\Large  BK \perp O'A' \Rightarrow BK \perp (OAA'O') \equiv (OAO')$ nên $\Large  d(B, (OAO')) = BK$

Xét tam giác O'A'B cân tại O' có $\Large O'A' = O'B = 2a; A'B = \dfrac{2a}{\tan \alpha}$

Gọi H là trung điểm A'B suy ra $\Large O'H \perp A'B$ nên

$\Large O'H = \sqrt{O'B^{2} - BH^{2}} = \sqrt{O'B^{2} - \dfrac{A'B^{2}}{4}} = \sqrt{4a^{2} - \dfrac{1}{4}.\dfrac{4a^{2}}{\tan^{2}\alpha}}= 2a\sqrt{1-\dfrac{1}{4\tan^{2}\alpha}}$

Mà $\Large BK.O'A' = O'H.A'B$ 

$\Large \Rightarrow BK = \dfrac{O'H.A'B}{O'A'} = \dfrac{2a\sqrt{1-\dfrac{1}{4\tan^{2}\alpha}}. \dfrac{2a}{\tan \alpha}}{2a} = 2a.\dfrac{1}{\tan \alpha}.\sqrt{1-\dfrac{1}{4\tan^{2}\alpha}}$

Do đó $\Large V_{OAO'B} = \dfrac{1}{3}.d(B,(OAO')).S_{OAO'}$ 

$\Large = \dfrac{1}{3} .2a.\dfrac{1}{\tan\alpha} \sqrt{1-\dfrac{1}{4\tan^{2}\alpha}} .2a^{2} = \dfrac{4a^{3}}{3}.\dfrac{1}{\tan\alpha}\sqrt{1-\dfrac{1}{4\tan^{2}\alpha}}$

Xét hàm số $\Large  y = \dfrac{1}{\tan \alpha} \sqrt{1-\dfrac{1}{4\tan^{2}\alpha}}$

Đặt $\Large t = \dfrac{1}{\tan \alpha}$ mà $\Large \tan\alpha = \dfrac{AA'}{A'B} = \dfrac{2a}{A'B}$ và $\Large  0 \leq A'B < 4a$ nên $\Large \dfrac{1}{2} \leq \tan \alpha < +\infty \Rightarrow t \in (0; 2]$

Ta được $\Large y = f(t) = t\sqrt{1-\dfrac{t^{2}}{4}} = \dfrac{t}{2}\sqrt{4-t^{2}}$
$\Large \Rightarrow f'(t)=\dfrac{1}{2}\left ( \sqrt{4-t^{2}}+t\dfrac{\left ( 4-t^2 \right )'}{2\sqrt{4-t^2}} \right )=\dfrac{4-2t^2}{2\sqrt{4-t^2}}\Leftrightarrow f'(t)=0\Leftrightarrow t=\pm \sqrt{2}$

Bảng biến thiên 

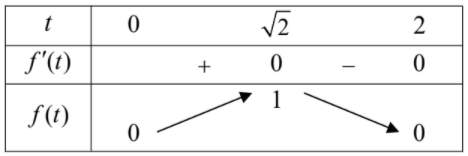
Vậy giá trị lớn nhất của $\Large V_{OAO'B}$ bằng $\Large \dfrac{4a^{3}}{3}$ khi $\Large t = \sqrt{2} \Rightarrow \dfrac{1}{\tan \alpha} = \sqrt{2} \Leftrightarrow \tan \alpha = \dfrac{1}{\sqrt{2}}$