Hàm số y = f(x) có đồ thị y = f'(x) như hình vẽ Xét hàm số $\Large g(x

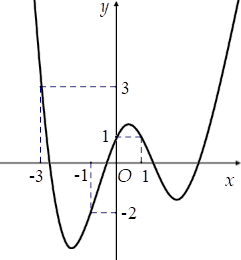
Hàm số y = f(x) có đồ thị y = f'(x) như hình vẽ

Xét hàm số $\Large g(x) = f(x) -\dfrac{1}{3}x^{3} - \dfrac{3}{4}x^{2} + \dfrac{3}{2}x + 2020$

Trong các mệnh đề dưới đây:

$\Large (I) g(0) < g(1)$

$\Large (II) \underset{[-3; 1]}{\min}\ g(x) = g(-1)$

$\Large (III)$ Hàm số $\Large  g(x)$ nghịch biến trên $\Large (-3; 1)$

$\Large (IV) \underset{[-3; 1]}{\max}\ g(x) = \max\left\{g(-3); g(1)\right\}$

Số mệnh đề đúng là:

• A. A. 4
• B. B. 3
• C. C. 2
• D. D. 1

$\Large g'(x) = f'(x) - \left(x^{2} + \dfrac{3}{2} x - \dfrac{3}{2}\right) = f'(x) - h(x),$ với $\Large h(x) = x^{2} + \dfrac{3}{2}x - \dfrac{3}{2}$

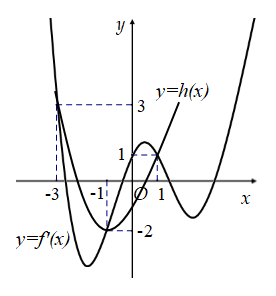
Từ hình vẽ ta có phương trình $\Large f'(x) - h(x) = 0$ có ba nghiệm trên đoạn $\Large [-3; 1]$ là x = {-3; -1; 1}

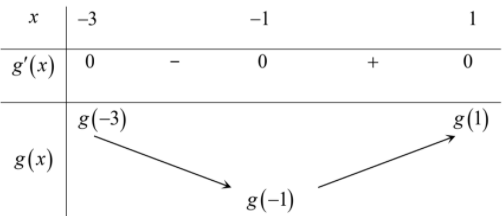
Suy ra các mệnh đề $\Large (I), (II), (IV)$ là mệnh đề đúng, mệnh đề $\Large (III)$ là mệnh đề sai