Cho hàm số $\Large f(x)$ liên tục trên $\Large \mathbb{R}$ và có bảng

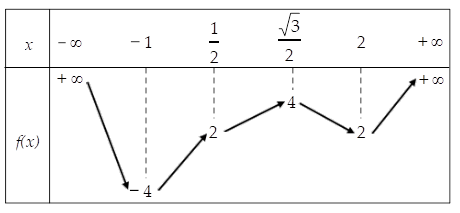
Cho hàm số $\Large f(x)$ liên tục trên $\Large \mathbb{R}$ và có bảng biến thiên như hình bên.

Số giá trị nguyên của tham số m để phương trình $\Large f^{2}(\cos x) + (3-m)f(\cos x)+ 2m-10 = 0$ có đúng 4 nghiệm phân biệt thuộc đoạn $\Large \left[-\dfrac{\pi}{3}; \pi\right]$ là

• A. A. 5
• B. B. 6
• C. C. 7
• D. D. 4

Ta có $\Large  f^{2}(\cos x) + (3-m) f(\cos x) + 2m - 10 = 0$

Đặt $\Large  t = f(\cos x)$ ta được phương trình $\Large t^{2} + (3-m)t + 2m -10 = 0 \Leftrightarrow$ $\Large \left[\begin{align}&t= 2\\&t = m-5\\\end{align}\right.$

$\Large \cdot$ Với $\Large t = 2 \Rightarrow f(\cos x) = 2 \Leftrightarrow$ $\Large \left[\begin{align}&\cos x = \dfrac{1}{2}\\&\cos x = 1\\\end{align}\right.$ $\Large \Leftrightarrow$ $\Large \left[\begin{align}&x = \pm\dfrac{\pi}{3}\\&x=0\\\end{align}\right.$ vì $\Large x \in \left[-\dfrac{\pi}{3}; \pi\right]$

$\Large \cdot$ Với $\Large t = m-5 \Rightarrow f(\cos x) = m-5 (1)$

Để phương trình ban đầu có 4 nghiệm phân biệt thuộc đoạn $\Large \left[-\dfrac{\pi}{3}; \pi\right]$ thì phương trình (1) có đúng 1 nghiệm trên đoạn $\Large \left[-\dfrac{\pi}{3}; \pi\right]$ khác $\Large -\dfrac{\pi}{3}; 0; \dfrac{\pi}{3}$.

Với $\Large x \in \left[-\dfrac{\pi}{3}; \pi\right] \Rightarrow u = \cos x \in [-1; 1]$

Nhận xét:

Nếu $\Large u\in \left[ \dfrac{1}{2}; 1\right)$ thì có 2 nghiệm $\Large x\in \left[-\dfrac{\pi}{3}; \pi\right]$

Nếu $\Large  u =1$ hoặc $\Large  u \in \left[ -1; \dfrac{1}{2}\right)$ thì có đúng 1 nghiệm $\Large x \in \left[-\dfrac{\pi}{3}; \pi\right]$

Do đó yêu cầu bài toán xảy ra khi và chỉ khi phương trình (1): 

$\Large f(\cos x) = m -5 \Leftrightarrow f(u) = m-5$ có nghiệm $\Large  u \in \left[-1; \dfrac{1}{2}\right)$. Từ bảng biến thiên suy ra $\Large -4 \leq m - 5 < 2 \Leftrightarrow 1 \leq m < 7$

Vì $\Large m \in \mathbb{R}$ nên $\Large m \in \left\{1; 2; 3; 4; 5; 6\right\}$