Tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc và có độ dài lần

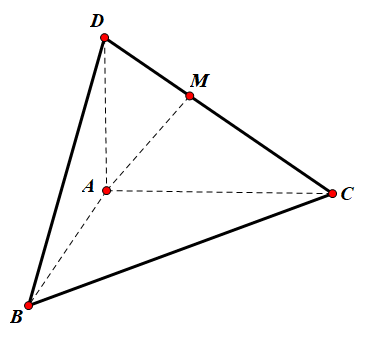
Tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc và có độ dài lần lượt là 2, 2 và 3. Gọi M là trung điểm của DC. Tính khoảng cách giữa hai đường thẳng AM và BC.

• A.

  $\Large \dfrac{\sqrt{22}}{6}$

• B.

  $\Large \dfrac{3 \sqrt{22}}{11}$

• C.

  $\Large \dfrac{\sqrt{3}}{2}$

• D.

  $\Large \dfrac{2 \sqrt{3}}{3}$

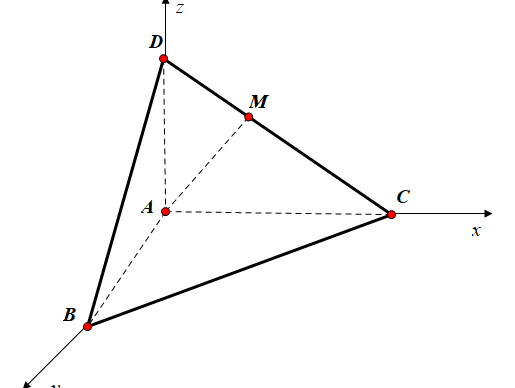
Ta chọn hệ tọa độ Axyz như hình vẽ với $\Large A(0 ; 0 ; 0), C(2 ; 0 ; 0), B(0 ; 2 ; 0) ; D(0 ; 0 ; 3)$

Vì M là trung điểm DC nên $\Large M\left(1 ; 0 ; \dfrac{3}{2}\right)$

$\Large \overrightarrow{A M}=\left(1 ; 0 ; \dfrac{3}{2}\right), \overrightarrow{B C}=(2 ;-2 ; 0) ; \overrightarrow{A C}=(2 ; 0 ; 0)$

$\Large [\overrightarrow{A M}, \overrightarrow{B C}]=(3 ; 3-2) \Rightarrow[\overrightarrow{A M}, \overrightarrow{B C}] \cdot \overrightarrow{A C}=6$

$\Large d(A M, B C)=\dfrac{|[\overrightarrow{A M}, \overrightarrow{B C}] \cdot \overrightarrow{A C}|}{|[\overrightarrow{A M}, \overrightarrow{B C}]|}=\dfrac{6}{\sqrt{9+9+4}}=\dfrac{3 \sqrt{22}}{11}$