Trên mặt phẳng tọa độ cho đường cong $\Large (C): y=x^{4}-4 x^{2}+2$ v

Trên mặt phẳng tọa độ cho đường cong $\Large (C): y=x^{4}-4 x^{2}+2$ và hai điểm $\Large A(-\sqrt{2} ; 0)$, $\Large B(\sqrt{2} ; 0)$, Có tất cả bao nhiêu điểm trên (C) mà tổng khoảng cách từ điểm đó đến các điểm A và B bằng $\Large 2 \sqrt{6}$?

• A. 3
• B. 7
• C. 6
• D. 1

Chon B

Xét điểm $\Large M \in(C): M A+M B=2 \sqrt{6}$, suy ra M thuộc elip $\Large (E): \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$

Hai tiêu điểm elip là $\Large A(-\sqrt{2} ; 0), B(\sqrt{2} ; 0) \Rightarrow c=\sqrt{2}$

Khi đó $\Large c=\sqrt{2} ; 2 a=2 \sqrt{6} \Rightarrow a=\sqrt{6} ; b=\sqrt{a^{2}-c^{2}}=2$ $\Large \Rightarrow(E): \dfrac{x^{2}}{6}+\dfrac{y^{2}}{4}=1$

Vẽ đường xong $\Large (C): y=x^{4}-4 x^{2}+2$ và elip thu được trên cùng một hệ trục tọa độ ta có

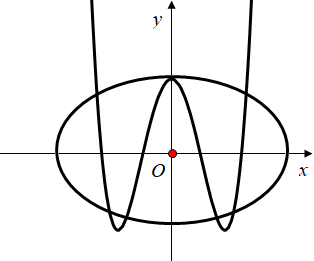
Kết luận 7 giao điểm dẫn đến tồn tại 7 điểm M.