Trong không gian với hệ trục tọa độ $\Large Oxyz$, cho mặt phẳng $\Lar

Trong không gian với hệ trục tọa độ $\Large Oxyz$, cho mặt phẳng $\Large (P):mx+2y-z+1=0$ (m là tham số). Mặt phẳng $\Large (P)$ cắt mặt cầu $\Large (S): (x-2)^{2}+(y-1)^{2}+z^{2}=9$ theo một đường tròn có bán kính bằng 2. Tìm tất cả các giá trị thực của tham số m?

• A. $\Large m=\pm1$
• B. $\Large m=\pm 2+\sqrt{5}$
• C. $\Large m=\pm 4$
• D. $\Large m=6\pm 2\sqrt{5}$

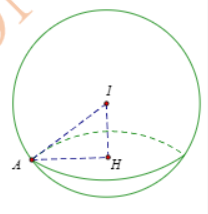
Từ $\Large (S): (x-2)^{2}+(y-1)^{2}+z^{2}=9$ ta có tâm $\Large I(2;1;0)$ bán kính R = 3. Gọi H là hình chiếu vuông góc của I trên (P) và $\Large (P)\cap (S)=C(H;r)$ với r = 2

Ta có $\Large IH=d(I;(P))\Leftrightarrow IH=\dfrac{|2m+2-0+1|}{\sqrt{m^{2}+4+1}=\dfrac{|2m+3|}{\sqrt{m^{2}+5}}$

Theo yêu cầu bài toán ta có $\Large R^{2}=IH^{2}+r^{2}\Leftrightarrow 9 =\dfrac{(2m+3)^{2}}{m^{2}+5}+4$

$\Large \Leftrightarrow m^{2}-12m+16=0\Leftrightarrow$ $\Large \left[\begin{align}&m=6-2\sqrt{5}\\&m=6+2\sqrt{5}\\\end{align}\right.$