Trong không gian $\Large Oxyz$, cho ba điểm $\Large A(-1;-4;4), B(1;7;

MỤC LỤC
Câu hỏi:
Trong không gian $\Large Oxyz$, cho ba điểm $\Large A(-1;-4;4), B(1;7;-2), C(1;4;-2)$. Mặt phẳng $\Large (P): 2x+by+cx+d=0$ qua A và thỏa mãn $\Large T = d(B,(P))+2d(C,(P))$ đạt giá trị lớn nhất. Tính b+c+d
Đáp án án đúng là: A
Lời giải chi tiết:
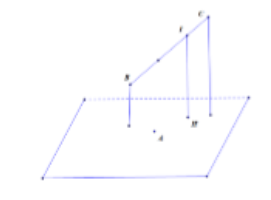
TH1: B, C cùng phía so với $\Large (P)$
Gọi I thỏa mãn $\Large \overrightarrow{IB}+2\overrightarrow{IC}=\overrightarrow{0}\Rightarrow I(1;5;-2)$
Có $\Large T=d(B,(P))+2d(C,(P))=3d(I,(P)) \leq 2IA$. $\Large MaxT=3IA$ khi $\Large IA \perp (P)\Rightarrow (P):2x+9y-6z+62=0\Rightarrow b+c+d=65$
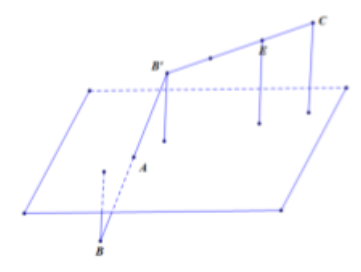
TH2: B, C khác phía so với (P)$
Gọi $\Large B'=D_A(B)\Rightarrow B'(-3;-15;10)$
Gọi E thỏa mãn $\Large \overrightarrow{EB'}+2\overrightarrow{EC}=\overrightarrow{O}\Rightarrow E\left(-\dfrac{1}{3};-\dfrac{7}{3};2\right)$
Có $\Large T=d(B,(P))+2d(C,(P))=d(B',(P))+2d(C,(P)) =3d(E,(P)) \leq 3EA$
$\Large MaxT=3EA$ khi $\Large EA\perp(P)\Rightarrow (P):2x+5y-6z+46=0\Rightarrow b+c+d=45$
Từ hai trường hợp suy ra khi $\Large T=d(B,(P))+2d(C,(P))$ đạt giá trị lớn nhất. Ta có $\Large b+c+d=65$
Xem thêm các bài tiếp theo bên dưới
- Biết rằng có n mặt phẳng có phương trình tương ứng là $\Large (P_1):x+
- Trong không gian $\Large Oxyz$, cho ba điểm $\Large A(3;0;0), B(1;2;1)
- Trong không gian cho đường thẳng $\Large \Delta:\dfrac{x-3}{1}=\dfrac{
- Cho số phức $\Large z=1-i+i^{3}$. Tìm phần thực a và phần ảo b của z.
- Cho $\Large z, z^{\prime}$ là hai số phức. Khẳng định nào sau đây là s