Trong không gian cho đường thẳng $\Large \Delta:\dfrac{x-3}{1}=\dfrac{

Trong không gian cho đường thẳng $\Large \Delta:\dfrac{x-3}{1}=\dfrac{y}{2}=\dfrac{z+1}{3}$ và đường thẳng $\Large d:\dfrac{x+3}{3}=\dfrac{y-1}{1}=\dfrac{z+2}{2}$. Viết phương trình mặt phẳng $\Large (P)$ đi qua $\Large \Delta$ vào tạo với đường thẳng d một góc lớn nhất

• A. $\Large 19x-17y-20z-77=0$
• B. $\Large 19x-17y-20z+34=0$
• C. $\Large 31x-8y-5z+91=0$
• D. $\Large 31x-8y-5z-98=0$

Đường thẳng $\Large d$ có VTCP là $\Large \overrightarrow{u_1}=(3;1;2)$

Đường thẳng $\Large \Delta$ đi qua điểm $\Large M(3;0;-1)$ và có VTCP là $\Large \overrightarrow{u}=(1;2;3)$

Do $\Large \Delta \subset (P)$ nên $\Large M\in (P).$ Giả sử VTPT của $\Large (P)$ là $\Large \overrightarrow{n}=(A,B,C), (A^{2}+B^{2}+C^{2})\neq 0)$

Phương trình $\Large (P)$ có dạng $\Large A(x-3)+By+C(z+1)=0$

Do $\Large \Delta \subset (P)$ nên $\Large \overrightarrow{u}.\overrightarrow{n}=0\Leftrightarrow A+2B+3C=0\Leftrightarrow A=-2B-3C$

Gọi $\Large \alpha$ là góc giữa $\Large d$ và $\Large (P)$. Ta có

$\Large \sin \alpha=\dfrac{|\overrightarrow{u_1}.\overrightarrow{n}|}{|\overrightarrow{u_1}|.|\overrightarrow{n}|}=\dfrac{|3A+B+2C|}{\sqrt{14}.\sqrt{A^{2}+B^{2}+C^{2}}}=\dfrac{|3(-2B-3C)+B+2C|}{\sqrt{14}.\sqrt{(-2B-3C)^{2}+B^{2}+C^{2}}}$

$\Large =\dfrac{|5B+7C|}{\sqrt{14}\sqrt{5B^{2}.12BC+10^{2}}}=\dfrac{1}{\sqrt{14}}\sqrt{\dfrac{(5B+7C)^{2}}{5B^{2}+12BC+10C^{2}}}$

TH1: Với $\Large C = 0$ thì $\Large \sin \alpha = \sqrt{\dfrac{5}{14}}=\sqrt{\dfrac{70}{14}}$

TH2: Với $\Large C\neq 0$ đặt $\Large t = \dfrac{B}{C}$ ta có $\Large \sin \alpha = \dfrac{1}{\sqrt{14}}\sqrt{\dfrac{(5t+7)^{2}}{5t^{2}+12t+10}}$

Xét hàm số $\Large f(t)=\dfrac{(5t+7)^{2}}{5t^{2}+12t+10} trên

Ta có $\Large f'(t)=\dfrac{-50t^{2}+10t+112}{(5t^{2}+12t+10)^{2}}$

$\Large f'(t)=0\Leftrightarrow -50t^{2}+10t+112=0\Leftrightarrow$ $\Large \left[\begin{align}&t=\dfrac{8}{5}\Rightarrow f\left(\dfrac{8}{5}\right)=\dfrac{75}{14}\\&t=-\dfrac{7}{5}\Rightarrow f\left(-\dfrac{7}{5}\right)=0\\\end{align}\right.$

Và $\Large \underset{lim}{x\rightarrow \pm \infty}f(t)=\underset{x\rightarrow \pm \infty}{lim}\dfrac{(5t+7)^{2}}{5t^{2}+12t+10}=5$

Bảng biến thiên 

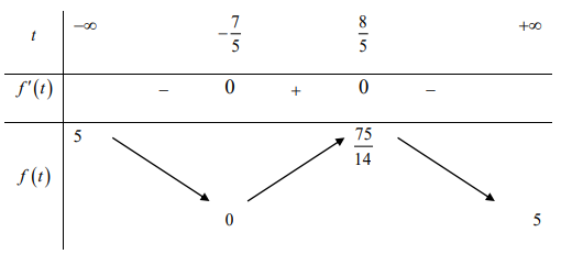
Từ đó ta có $\Large max\ f(t)=\dfrac{75}{14}$ khi $\Large t=\dfrac{8}{5}\Rightarrow \dfrac{B}{C}=\dfrac{8}{5}$. Khi đó $\Large \sin \alpha =\dfrac{1}{\sqrt{14}}.\sqrt{f\left(\dfrac{8}{5}\right)}=\dfrac{\sqrt{75}}{14}$

So sánh TH1 và TH2 ta có $\Large \sin \alpha$ lớn nhất là $\Large \sin \alpha =\dfrac{\sqrt{75}}{14}$ khi $\Large \dfrac{B}{C}=\dfrac{8}{5}$

Chọn $\Large B = -8 \Rightarrow C = -5 \Rightarrow A = 31$

Phương trinhd $\Large (P)$ là $\Large 31(x-3)-8y-5(z+1)=0\Leftrightarrow 31x-8y-5z-98=0$