Trong không gian với hệ trục tọa độ $\Large Oxyz$, cho đường thẳng $\L

Trong không gian với hệ trục tọa độ $\Large Oxyz$, cho đường thẳng $\Large \Delta:\dfrac{x-1}{1}=\dfrac{y-1}{2}=\dfrac{z}{2}$ và mặt phẳng $\Large (\alpha):x-2y+2z-5=0$. Gọi $\Large (P)$ là mặt phẳng chứa $\Large \Delta$ và tạo với $\Large (\alpha)$ một góc nhỏ nhất. Phương trình mặt phẳng $\Large (P)$ có dạng $\Large ax+by+cz+d=0(a,b,c,d\in \mathbb{Z}$ và $\Large a,b,c,d<5)$. Khi đó tích a.b.c.d bằng bao nhiêu?

• A. -60
• B. 120
• C. 60
• D. -120

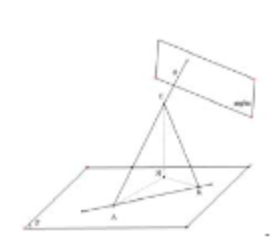
Trên đường thẳng $\Large \Delta$ lấy điểm A(1;1;0). Gọi d là đường thẳng đi qua A và vuông góc với mặt phẳng $\Large (\alpha)$. Ta có $\Large \overrightarrow{u_d}=(1;-2;2)$

Trên đường thẳng d lấy điểm C bất kì khác điểm A

Gọi H, K lần lượt là hình chiếu vuông góc của C lên mặt phẳng $\Large (P)$ và đường thẳng $\Large \Delta$

Lúc này, ta có $\Large ((P);(\alpha))=(CH;d)=\widehat{HCA}$

Xét tam giác HCA ta có $\Large \sin\widehat{HCA}=\dfrac{AH}{AC}$, mà tam giác AHK vuông tại K nên ta có $\Large \dfrac{AH}{AC}\geq \dfrac{AK}{AC}$ (không đổi). Nên để góc $\Large \widehat{HCA}$ nhỏ nhất khi H trùng với K hay $\Large CK\perp (P)$

Ta có $\Large (ACK)$ đi qua d và $\Large \Delta$, vuông góc mặt phẳng (ACK) và $\Large \left[\overrightarrow{n_{(ACK)};\overrightarrow{u_\Delta}\right]=(-2;5;-4)$

Nên $\Large \overrightarrow{n_{(P)}} = (-2;5;-4)$. Vậy phương trình mặt phẳng $\Large (P)$ là:

$\Large -2(x-1)+5(y-1)-4z=0\Leftrightarrow -2x+5y-4z-3=0\Leftrightarrow 2x-5y+4z+3=0$

Vậy a.b.c.d=2.(-5).4.3=-120