Trong không gian với hệ tọa độ $\Large Oxyz$ cho hai điểm $\Large A(1;

Trong không gian với hệ tọa độ $\Large Oxyz$ cho hai điểm $\Large A(1;2;-3), B(-2;-2;1)$ và mặt phẳng $\Large (\alpha):2x+2y-z+9=0$. Gọi M là điểm thay đổi trên mặt phẳng $\Large (\alpha)$ sao cho M luôn nhìn đoạn AB dưới một góc vuông. Xác định phương trình đường thẳng MB khi MB đạt giá trị lớn nhất.

• A. $\Large \left\{\begin{align}&x=-2-t\\&y=-2+2t\\&z=1+2t\\\end{align}\right.$
• B. $\Large \left\{\begin{align}&x=-2+2t\\&y=-2-t\\&z=1+2t\\\end{align}\right.$
• C. $\Large \left\{\begin{align}&x=-2+t\\&y=-2\\&z=1+2t\\\end{align}\right.$
• D. $\Large \left\{\begin{align}&x=-2+t\\&y=-2-t\\&z=1\\\end{align}\right.$

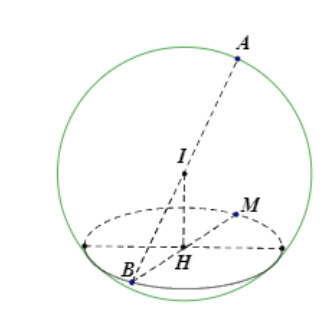
Ta có $\Large M\in (\alpha)$ và $\Large \widehat{AMB}=90^{o}$ suy ra M nằm trên đường tròn (C) là giao tuyến của mặt phẳng $\Large (\alpha)$ và mặt cầu (S) đường kính AB

Lại có $\Large B\in (\alpha)$ suy ra B và M cùng nằm trên đường tròn (C)

Khi đó MB lớn nhất khi và chỉ khi MB là đường kính của đường tròn (C)

Gọi I là tâm mặt cầu (S) suy ra $\Large I\left(-\dfrac{1}{2};0;-1\right)$, H là tâm đường tròn (C)

$\Large (\alpha)$ có một vecto pháp tuyến là $\Large \overrightarrow{n_(\alpha)}(2;2;-1)$

Đường thẳng IH vuông góc với $\Large (\alpha)$ nên nhận $\Large \overrightarrow{n_{(\alpha)}(2;2;-1)$ là vecto chỉ phương 

Phương trình tham số của đường thẳng IH: $\Large \left\{\begin{align}&x=-\dfrac{1}{2}+2t\\&y=2t\\&z=-1-t\\\end{align}\right.$

Ta có $\Large H\left(-\dfrac{1}{2}+2t;2t;-1-t\right)$

$\Large H\in (\alpha) \Leftrightarrow 2\left(-\dfrac{1}{2}+2t\right)+2(2t)-(-1-t)+9=0\Leftrightarrow t = -1$. Suy ra $\Large H\left(-\dfrac{5}{2};-2;0\right)$

Phương trình đường thẳng BM đi qua B nhận $\Large \overrightarrow{BH}=\left(-\dfrac{1}{2};0;-1\right)=-\dfrac{1}{2}(1;0;2)$ làm vecto chỉ phương là: $\Large \left\{\begin{align}&x=-2+t\\&y=-2\\&z=1+2t\\\end{align}\right.$