Trong không gian với hệ trục tọa độ $\Large Oxyz$ cho ba mặt phẳng $\L

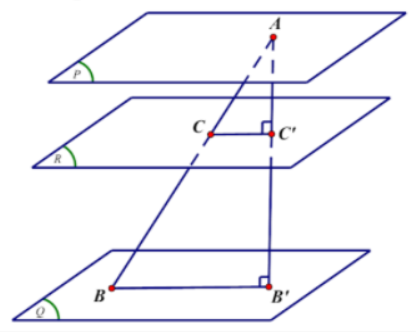
Trong không gian với hệ trục tọa độ $\Large Oxyz$ cho ba mặt phẳng $\Large (P):x-2y+z-1=0, (Q): x-2y+z+8=0, (R): x-2y+z-4=0$. Đường thẳng d thay đổi cắt ba mặt phẳng $\Large (P), (Q), (R)$ lần lượt tại $\Large A, B, C$. Tìm giá trị nhỏ nhất của $\Large T=AB^{2}+\dfrac{144}{AC}$

• A. $\Large 72\sqrt[3]{3}$
• B. $\Large 96$
• C. $\Large 108$
• D. $\Large 72\sqrt[3]{4}$

Ta có $\Large M(1;0;0)\in (P)$ và ba mặt phẳng $\Large (P),(Q),(R)$ đôi một song song với nhau.

Gọi $\Large B',C'$ lần lượt là hình chiếu vuông góc của A trên các mặt phẳng $\Large (Q),(R)$, ta có:

$\Large AB'=d(A;(Q))=d(M;(Q))=\dfrac{|1-2.0+0+8|}{\sqrt{1^{2}+(-2)^{2}+1^{2}}}=\dfrac{3\sqrt{6}}{2}$

$\Large AC'=d(A;(R))=d(M;(R))=\dfrac{|1-2.0+0-4|}{\sqrt{1^{2}+(-2)^{2}+1^{2}}}=\dfrac{\sqrt{6}}{2}$

Do $\Large AB'=3AC'$ nên đặt $\Large CC'=a\Rightarrow BB'=3a$

Ta có $\Large AB^{2}=AB'^{2}+BB'^{2}=\dfrac{27}{2}+9a^{2};AC=\sqrt{AC'^{2}+CC'^{2}}=\sqrt{\dfrac{3}{2}+a^{2}}$

Nên $\Large T=AB^{2}+\dfrac{144}{AC}=\dfrac{27}{2}+9a^{2}+\dfrac{144}{\sqrt{\dfrac{3}{2}+a^{2}}}=9\left(\dfrac{3}{2}+a^{2}\right)+\dfrac{72}{\sqrt{\dfrac{3}{2}+a^{2}}}+\dfrac{72}{\sqrt{\dfrac{3}{2}+a^{2}}}$

$\Large \geq 3\sqrt[3]{9\left(\dfrac{3}{2}+a^{2}\right).\dfrac{72}{\sqrt{\dfrac{3}{2}+a^{2}}}.\dfrac{72}{\sqrt{\dfrac{3}{2}+a^{2}}}}=108$

Do đó $\Large minT=108$ khi $\Large a=\dfrac{\sqrt{2}}{2}$