Trong không gian với hệ tọa độ $\Large Oxyz$, cho mặt phẳng $\Large (P

Trong không gian với hệ tọa độ $\Large Oxyz$, cho mặt phẳng $\Large (P): 2x+2y-z+4=0$ và các điểm A(2;1;2), B(3;-2;2). Điểm M thuộc mặt phẳng $\Large (P)$ sao cho các đường thẳng MA, MB luôn tạo với mặt phẳng $\Large (P)$ các góc bằng nhau. Biết rằng điểm M luôn thuộc đường tròn $\Large (C)$ cố định. Tìm tọa độ tâm của đường tròn $\Large (C)$

 

• A. $\Large \left(\dfrac{74}{27};-\dfrac{97}{27};\dfrac{62}{27}\right)$
• B. $\Large \left(\dfrac{10}{3};-3;\dfrac{14}{3}\right)$
• C. $\Large \left(\dfrac{17}{21};-\dfrac{17}{21};\dfrac{17}{21}\right)$
• D. $\Large \left(\dfrac{32}{9};-\dfrac{49}{9};\dfrac{2}{9}\right)$

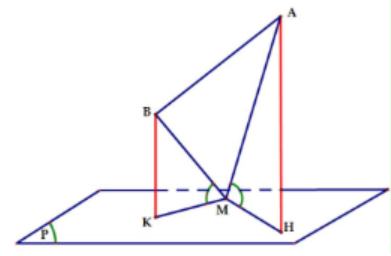
Gọi H, K lần lượt là hình chiếu vuông góc của A, B lên $\Large (P)$

Ta có tọa độ H thỏa mãn $\Large \left\{\begin{align}&AH:\dfrac{x-2}{2}=\dfrac{y-1}{2}=\dfrac{z-2}{-1}\\&(P): 2x+2y-z+4=0\\\end{align}\right.$ $\Large \Rightarrow H\left(\dfrac{2}{9};-\dfrac{7}{9};\dfrac{26}{9}\right)$

Tương tự tọa độ K thỏa $\Large \left\{\begin{align}&BK:\dfrac{x-3}{2}=\dfrac{y+2}{2}=\dfrac{z-2}{-1}\\&(P):2x+2y-z+4=0\\\end{align}\right.$ $\Large \Rightarrow K\left(\dfrac{19}{9};-\dfrac{26}{9};\dfrac{22}{9}\right)$

Theo giả thiết ta có

$\Large \measuredangle BMK=\measuredangle AMH \Rightarrow \tan \measuredangle BMK = \tan \measuredangle AMH \Rightarrow \dfrac{BK}{MK}=\dfrac{AH}{MH}\Rightarrow \dfrac{MK}{MH}=\dfrac{d(B;(P))}{d(A;(P))}=\dfrac{1}{2}$

$\Large \Rightarrow MH=2MK\Rightarrow MH^{2}=4MK^{2}\Rightarrow (\overrightarrow{MI}+\overrightarrow{IH})^{2}=4(\overrightarrow{MI}+\overrightarrow{IK})^{2}$

$\Large \Rightarrow 2\overrightarrow{MI}.\overrightarrow{IH}+IH^{2}=3MI^{2}+8\overrightarrow{MI}.\overrightarrow{IK}+4IK^{2}$

$\Large \Rightarrow 3MI^{2}=4IK^{2}-IH^{2}+2\overrightarrow{MI}(4\overrightarrow{IK}-\overrightarrow{IH})$

Gọi I là điểm sao cho $\Large \overrightarrow{IH}=4\overrightarrow{IK}$. Khi đó $\Large MI^{2}=\dfrac{4IK^{2}-IH^{2}}{3}$ hay M thuộc vào mặt cầu tâm I có bán kính $\Large \sqrt{\dfrac{4IK^{2}-IH^{2}}{3}}$ với $\Large I\left(\dfrac{74}{27};-\dfrac{97}{27};\dfrac{62}{27}\right)$

Khi đó $\Large M\in (C)=(S)\cap(P)$. Do đó, tâm đường tròn cần tìm là hình chiếu của I lên (P).

Nhận xét $\Large I\in (P)$, do đó tâm đường tròn cũng chính là tâm mặt cầu