Trong không gian với hệ tọa độ OxyzOxyz, mặt phẳng $\Large (\alph

MỤC LỤC
Câu hỏi:
Trong không gian với hệ tọa độ OxyzOxyz, mặt phẳng (α)(α) đi qua điểm M(1;2;1)M(1;2;1) và cắt các tia Ox,Oy,OzOx,Oy,Oz lần lượt tại A,B,CA,B,C sao cho độ dài OA,OB,OCOA,OB,OC theo thứ tự tạo thành một cấp số nhân có công bội bằng 2. Tính khoảng cách từ gốc tọa độ O tới mặt phẳng (α)(α)
Đáp án án đúng là: C
Lời giải chi tiết:
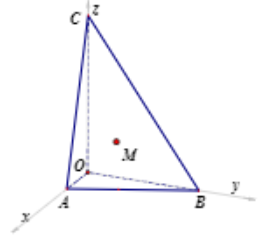
Đặt OA=a(a>0)OA=a(a>0). Khi đó OB=2a,OC=4aOB=2a,OC=4a
Áp dụng phương trình mặt phẳng theo đoạn chắn ta có mặt phẳng (α)(α) có phương trình xa+y2a+z4a=1xa+y2a+z4a=1
Do M(1;2;1)∈(α)M(1;2;1)∈(α) nên 1a+22a+14a=1⇔94a=1⇔a=941a+22a+14a=1⇔94a=1⇔a=94 (thỏa mãn a>0a>0)
Phương trình tổng quát của mặt phẳng (α)(α) là: 4x+2y+z−9=04x+2y+z−9=0
Suy ra d(O;(α))=|4.0+2.0+0−9|√42+22+12=3√217d(O;(α))=|4.0+2.0+0−9|√42+22+12=3√217
Xem thêm các bài tiếp theo bên dưới
- Đường thẳng ΔΔ song song với $\Large d:\dfrac{x+4}{3}=\df
- Trong không gian OxyzOxyz cho đường thẳng $\Large d:\dfrac{x-1}{2
- Trong không gian với hệ trục tọa độ OxyzOxyz, cho tứ diện $\Large
- Trong không gian với hệ tọa độ OxyzOxyz, cho hai điểm $\Large A(5
- Trong không gian OxyzOxyz, cho bốn điểm $\Large A(-4;-1;3), B(-1;