Trong không gian với hệ trục tọa độ $\Large Oxyz$, cho tứ diện $\Large

Trong không gian với hệ trục tọa độ $\Large Oxyz$, cho tứ diện $\Large ABCD$ có tọa độ các điểm $\Large A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4)$. Trên các cạnh $\Large AB,AC,AD$ lần lượt lấy các điểm $\Large B',C',D'$ sao cho $\Large \dfrac{AB}{AB'}+\dfrac{AC}{AC'}+\dfrac{AD}{AD'}=4$ và tứ diện $\Large AB'C'D'$ có thể tích nhỏ nhất. Phương trình mặt phẳng $\Large (B'C'D')$ là

• A. $\Large 16x-40y-44z+39=0$
• B. $\Large 16x-40y-44z-39=0$
• C. $\Large 16x+40y+44z-39=0$
• D. $\Large 16x+40y-44z+39=0$

Trên các cạnh $\Large AB, AC, AD$ của tứ diện $\Large ABCD$ lần lượt có các điểm $\Large B',C',D'$. Áp dụng công thức tỉ số thể tích ta có $\Large \dfrac{V_{AB'C'D'}}{V_{ABCD}}=\dfrac{AB'}{AB}.\dfrac{AC'}{AC}.\dfrac{AD'}{AD}$

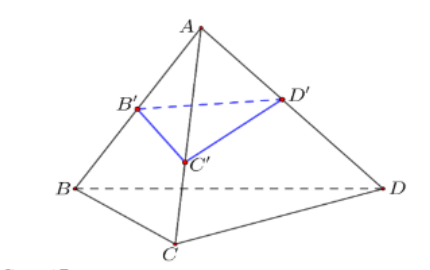
Từ giả thiết $\Large \dfrac{AB}{AB'}+\dfrac{AC}{AC'}+\dfrac{AD}{AD'}=4$, áp dụng bất đẳng thức $\Large AM-GM$ ta có:

$\Large 4=\dfrac{AB}{AB'}+\dfrac{AC}{AC'}+\dfrac{AD}{AD'}\leq 3\sqrt[3]{\dfrac{AB}{AB'}.\dfrac{AC}{AC'}.\dfrac{AD}{AD'}}=3\sqrt[3]{\dfrac{V_{ABCD}}{V_{AB'C'D'}}}$

$\Large \Leftrightarrow 64 \leq 27.\dfrac{V_{ABCD}}{V_{AB'C'D'}}\Leftrightarrow V_{AB'C'D'}\leq \dfrac{27}{64}V_{ABCD}$

Do $\Large V_{ABCD}$ cố định nên $\Large V_{AB'C'D'}$ nhỏ nhất $\Large \Leftrightarrow V_{A'B'C'D'}=\dfrac{27}{64}V_{ABCD}\Leftrightarrow \dfrac{AB}{AB'}=\dfrac{AC}{AC'}=\dfrac{AD}{AD'}=\dfrac{4}{3}$

$\Large \Leftrightarrow \dfrac{AB'}{AB}=\dfrac{AC'}{AC}=\dfrac{AD'}{AD}=\dfrac{3}{4}$

$\Large \Leftrightarrow (B'C'D')$ song song với $\Large (BCD)$ và đi qua điểm $\Large B'$ thỏa $\Large \overrightarrow{AB'}=\dfrac{3}{4}\overrightarrow{AB}$

Có $\Large \overrightarrow{BC}=(-3;-1;-2),\overrightarrow{BD}=(-2;3;2)$, suy ra vecto pháp tuyến của mặt phẳng $\Large (B'C'D')$ là $\Large \overrightarrow{n}=[\overrightarrow{BC},\overrightarrow{BD}]=(4;10;-11)$

Có $\Large \overrightarrow{AB}=(1;-1;1)$, giả sử $\Large B'(x;y;z)$. Do $\Large \overrightarrow{AB'}=\dfrac{3}{4}\overrightarrow{AB}$ nên $\Large B\left(\dfrac{7}{4};\dfrac{1}{4};\dfrac{7}{4}\right)$

Vậy phương trình $\Large (B'C'D')$ là: 16x+40y-44z+39=0$