Trong không gian với hệ tọa độ $\Large Oxyz$, cho hai điểm $\Large A(5

Trong không gian với hệ tọa độ $\Large Oxyz$, cho hai điểm $\Large A(5;0;0)$ và $\Large B(3;4;0)$. Với C là điểm nằm trên trục $\Large Oz$, gọi $\Large H$ là trực tâm của tam giác $\Large ABC$. Khi $\Large C$ di động trên trục $\Large Oz$ thì $\Large H$ luôn thuộc một đường tròn cố định. Bán kính của đường tròn đó bằng

• A. $\Large \dfrac{\sqrt{5}}{4}$
• B. $\Large \dfrac{\sqrt{3}}{2}$
• C. $\Large \dfrac{\sqrt{5}}{2}$
• D. $\Large \sqrt{3}$

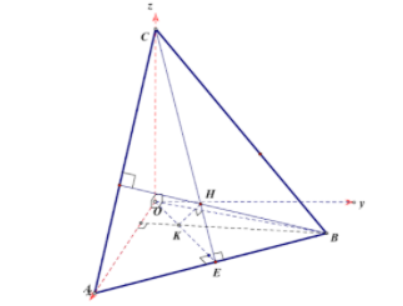Ta có $\Large C(0;0;c)$. Dễ thấy tam giác $\Large ABC$ cân tại $\Large C$. Gọi $\Large E(4;2;0)$ là trung điểm của $\Large AB$

Ta có mặt phẳng $\Large (OCE)$ vuông góc với $\Large AB$ (do $\Large \left\{\begin{align}&AB\perp OC\\&AB\perp CE\\\end{align}\right.$) và là mặt phẳng cố định.

Gọi $\Large K$ là trực tâm tam giác $\Large OAB$, do $\Large A, B$ và $\Large K$ cùng nằm trong mặt phẳng $\Large (Oxy)$ nên $\Large \left\{\begin{align}&\overrightarrow{OK}.\overrightarrow{AB}=0\\&\overrightarrow{BK}.\overrightarrow{OA}=0\\\end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align}&x.(-2)+y.4=0\\&x-3=0\\\end{align}\right.$ $\Large \Leftrightarrow \left\{\begin{align}&x=3\\&y=\dfrac{3}{2}\\\end{align}\right.$. Tìm được $\Large K=\left(3;\dfrac{3}{2};0\right)$

Ta chứng minh được $\Large KH\perp(CAB)$ do $\Large \left\{\begin{align}&AB\perp(OEC)\\&CA\perp (BHK)\\\end{align}\right.$ $\Large \Rightarrow \left\{\begin{align}&HK\perp AB\\&HK\perp CA\\\end{align}\right.$

Suy ra $\Large \widehat{KHE}=90^{o}$. Suy ra $\Large H$ thuộc mặt cầu đường kính $\Large KE=\sqrt{1+\dfrac{1}{4}}=\dfrac{\sqrt{5}}{2}$ và $\Large \Rightarrow d(B,(SCD))=\dfrac{3}{2}d(H,(SCD))$ thuộc mặt phẳng $\Large (OCE)$ cố định. Vậy $\Large H$ luôn thuộc một đường tròn cố định có bán kính $\Large R=\dfrac{\sqrt{5}}{4}$