Trong không gian với hệ tọa độ $\Large Oxyz$, cho hai đường thẳng $\La

Trong không gian với hệ tọa độ $\Large Oxyz$, cho hai đường thẳng $\Large d_1:\dfrac{x-1}{1}=\dfrac{y+2}{2}=\dfrac{z}{-1}$ và $\Large d_2:\dfrac{x+2}{2}=\dfrac{y-1}{-1}=\dfrac{z}{2}$. Phương trình mặt phẳng $\Large (P)$ chứa $\Large (d_1)$ sao cho góc giữa $\Large (P)$ và đường thẳng $\Large (d_2)$ là lớn nhất là $\Large ax-y+cz+d=0$. Giá trị của biểu thức $\Large T=a+c+d$ bằng

• A. $\Large T=-6$
• B. $\Large T=0$
• C. $\Large T=3$
• D. $\Large T=-\dfrac{13}{4}$

Ta xét bài toán tổng quát như sau:

Bài toán: Cho hai đường thẳng $\Large d_1,d_2$ không song song. Viết phương trình mặt phẳng $\Large (P)$ chứa $\Large d_1$ và tạo với đường thẳng $\Large d_2$ một góc lớn nhất.

Phương pháp giải:

Giả sử $\Large d_1$ có vecto chỉ phương $\Large \overrightarrow{u_1},d_2$ có vecto chỉ phương $\Large \overrightarrow{u_2}$

Trước hết ta xét trường hợp $\Large d_1$ và $\Large d_2$ chéo nhau.

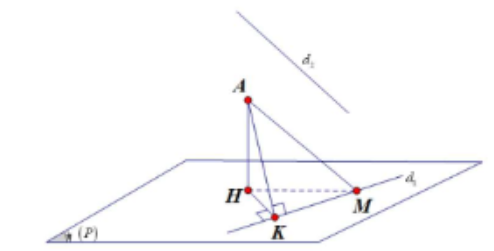
Gọi $\Large M$ là một điểm nào đó thuộc $\Large d_1$, dựng đường thẳng qua $\Large M$ và song song với $\Large d_2$. Lấy điểm $\Large A$ cố định trên đường thẳng đó. Gọi $\Large H$ là hình chiếu của $\Large A$ lên mặt phẳng $\Large P, K$ là hình chiếu của $\Large A$ lên đường thẳng $\Large d_1$

Góc giữa mặt phẳng $\Large (P)$ và đường thẳng $\Large d_1$ là $\Large \widehat{AMH}$

Ta có $\Large \sin(\widehat{d_2,P})=\sin(\widehat{HMA})=\dfrac{AH}{AM}\leq \dfrac{AK}{AM}$ (do $\Large AH\leq AK$). Góc $\Large (\widehat{d_2,P})$ lớn nhất khi $\Large \sin(\widehat{d_2,P})$ lớn nhất. Do $\Large \dfrac{AK}{AM}$ không đổi suy ra $\Large \sin(\widehat{d_2,P})$ lớn nhất $\Large H\equiv K$

Mặt phẳng $\Large (P)$ cần tìm là mặt phẳng chứa $\Large d_1$ và vuông góc với mặt phẳng $\Large (AKM)$, hay vecto pháp tuyến của $\Large (P)$ vuông góc với hai vecto $\Large \overrightarrow{u_1}$ và $\Large [\overrightarrow{u_1},\overrightarrow{u_2}]$.

Nên ta chọn vecto pháp tuyến của $\Large (P)$ là $\Large \overrightarrow{n_{(P)}}=[\overrightarrow{u_1},[\overrightarrow{u_1},\overrightarrow{u_2}]]$.

Trường hợp $\Large d_1$ và $\Large d_2$ cắt nhau tại M, bài toàn giải tương tự như trên. Kết luận không thay đổi vecto pháp tuyến của $\Large (P)$ là $\Large \overrightarrow{n_{(P)}}=[\overrightarrow{u_1},[\overrightarrow{u_1},\overrightarrow{u_2}]]$

Áp dụng vào bài 45 ta có $\Large \overrightarrow{u_1}=(1;2;-1);\overrightarrow{u_2}=(2;-1;2)$

$\Large \Rightarrow [\overrightarrow{u_1};\overrightarrow{u_2}]=(3;-4;-5)\Rightarrow \overrightarrow{n_{(P)}}=[\overrightarrow{u_1},[\overrightarrow{u_1},\overrightarrow{u_2}]]=(-14;2;-10)=-2(7;-1;5)$

Mặt phẳng $\Large (P)$ chứa $\Large d_1$ nên mặt phẳng $\Large (P)$ đi qua điểm $\Large A(1;-2;0)$

Phương trình mặt phẳng $\Large (P):7x-y+5z-9=0$. Suy ra $\Large a+c+d=7+5-9=3$