Trong không gian với hệ tọa độ $\Large Oxyz$, cho hình thang ABCD có đ

Trong không gian với hệ tọa độ $\Large Oxyz$, cho hình thang ABCD có đáy AB, CD; có tọa độ ba đỉnh $\Large A(1;2;1), B(2;0;-1), C(6;1;0)$. Biết hình thang có diện tích bằng $\Large 6\sqrt{2}$. Giả sử đỉnh $\Large D(a;b;c)$, tìm mệnh đề đúng?

• A. $\Large a+b+c=6$
• B. $\Large a+b+c=5$
• C. $\Large a+b+c=8$
• D. $\Large a+b+c=7$

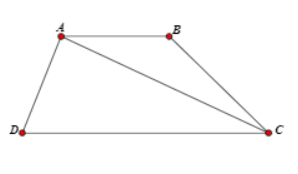
Ta có $\Large AB=3,h=d(C,AB)=\dfrac{\sqrt{162}}{3}$

$\Large S_{ABCD}=\dfrac{h}{2}(AB+CD)\Leftrightarrow 6\sqrt{2}=\dfrac{\sqrt{162}}{6}(3+CD)\Leftrightarrow CD=1$

Suy ra $\Large \overrightarrow{AB}=3\overrightarrow{DC}\Leftrightarrow D\left(\dfrac{17}{3};\dfrac{5}{3};\dfrac{2}{3}\right)\Rightarrow a+b+c=8$