Trong không gian với hệ tọa độ $\Large Oxyz$, cho bốn điểm $\Large A(1

Trong không gian với hệ tọa độ $\Large Oxyz$, cho bốn điểm $\Large A(1;-2;0), B(0;-1;1), C(2;1;-1), D(3;1;4)$. Hỏi có bao nhiêu mặt phẳng cách đều bốn điểm đó?

• A. 1
• B. 4
• C. 7
• D. Vô số

Ta có $\Large \overrightarrow{AB}=(-1;1;1), \overrightarrow{AC}=(1;3;-1), \overrightarrow{AD}=(2;3;4)$

Khi đó $\Large [\overrightarrow{AB},\overrightarrow{AC}]=(-4;0;-4)$ suy ra $\Large \overrightarrow{AB},\overrightarrow{AC}].\overrightarrow{AD}=-24\neq 0$

Khi đó A, B, C, D không đồng phẳng và là 4 đỉnh của một tứ diện

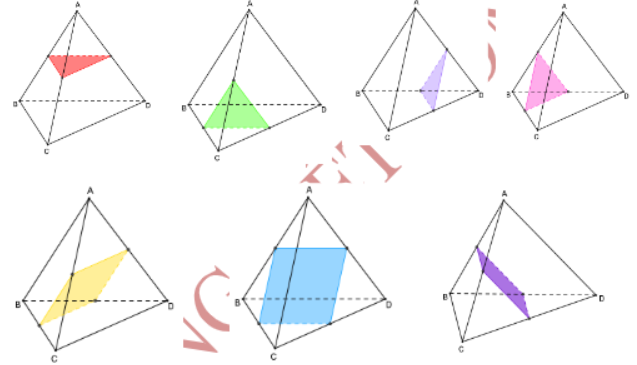
Khi đó sẽ có 7 mặt phẳng cách đều bốn đỉnh của tứ diện. Bao gồm: 4 mặt phẳng đi qua trung điểm của ba cạnh tứ diện và 3 mặt phẳng đi qua trung đểm bốn cạnh tứ diện (như hình vẽ)