Trong không gian với hệ tọa độ $\Large Oxyz$, cho điểm A(1;2;-3) và mặ

Trong không gian với hệ tọa độ $\Large Oxyz$, cho điểm A(1;2;-3) và mặt phẳng $\Large (P):2x+2y-z+9=0$. Đường thẳng d đi qua A và có vecto chỉ phương $\Large \overrightarrow{u}=(3;4;-4)$ cắt $\Large (P)$ tại B. Điểm M thay đổi trong $\Large (P)$ sao cho M luôn nhìn đoạn AB dưới góc $\Large 90^{o}$. Khi độ dài MB lớn nhất, đường thẳng MB đi qua điểm nào trong các điểm sau?

• A. $\Large H(-2;-1;3)$
• B. $\Large I(-1;-2;3)$
• C. $\Large K(3;0;15)$
• D. $\Large J(-3;2;7)$

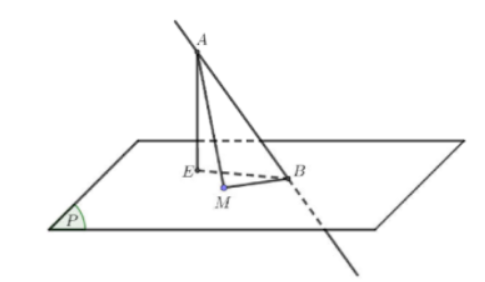
+ Đường thẳn d đi qua A(1;2;-3) và có vecto chỉ phương $\Large \overrightarrow(3;4;-4)$ có phương trình là $\Large \left\{\begin{align}&x=1+3t\\&y=2+4t\\&z=-3-4t\\\end{align}\right.$

+ Ta có: $\Large MB^{2}=AB^{2}-MA^{2}$. Do đó $\Large (MB)_{max}$ khi và chỉ khi $\Large (MA)_{min}$

+ Gọi E là hình chiếu của A lên $\Large (P)$. Ta có $\Large AM \geq AE$

Đẳng thức xảy ra khi và chỉ khi $\Large M\equiv E$

Khi đó $\Large (MA)_{max}=AE$ và MB qua B nhận $\Large \overrightarrow{BE}$ làm vecto chỉ phương

+ Ta có: $\Large B\in d$ nên $\Large B(1+3t;2+4t;-3-4t)$ mà $\Large B\in(P)$ suy ra:

$\Large 2(1+3t)+2(2+4t)-(-3-4t)+9=0\Leftrightarrow t = -1\Leftrightarrow B(-2;-2;-1)$

+ Đường thẳng AE qua $\Large A(1;2;-3)$, nhận $\Large \overrightarrow{n_P}=(2;2;-1)$ làm vecto chỉ phương có phương trình là $\Large \left\{\begin{align}&x=1+2t\\&y=2+2t\\&z=-3-t\\\end{align}\right.$

Suy ra $\Large E(1+2t;2+2t;-3-t)$

Mặt khác, $\Large E\in(P)$ nên $\Large 2(1+2t)+2(2+2t)-(-3-t)+9=0\Leftrightarrow t = -2\Leftrightarrow E(-3;-2;-1)$ 

+ Do đó đường thẳng MV qua B(-2;-2;1), có vecto chỉ phương $\Large \overrightarrow{BE}=(-1;0;-2)$ nên có phương trình là $\Large \left\{\begin{align}&x=-2-t\\&y=-2\\&z=1-2t\\\end{align}\right.$

Thử các đáp án thấy điểm $\Large I(-1;-2;3)$ thỏa mãn