Trong không gian $\Large Oxyz$, cho tam giác nhọn ABC có $\Large H(2;2

Trong không gian $\Large Oxyz$, cho tam giác nhọn ABC có $\Large H(2;2;1), K\left(-\dfrac{8}{3};\dfrac{4}{3};\dfrac{8}{3}\right),O$ lần lượt là hình chiếu vuông góc của A, B, C trên các cạnh BC, AC, AB. Đường thẳng d qua A và vuông góc vưới mặt phẳng (ABC) có phương trình là

• A. $\Large \dfrac{x+4}{1}=\dfrac{y+1}{-2}=\dfrac{z-1}{2}$
• B. $\Large \dfrac{x-\dfrac{8}{3}}{1}=\dfrac{y-\dfrac{2}{3}}{-2}=\dfrac{z+\dfrac{2}{3}}{2}$
• C. $\Large \dfrac{x+\dfrac{4}{9}}{1}=\dfrac{y-\dfrac{17}{9}}{-2}=\dfrac{z-\dfrac{19}{9}}{2}$
• D. $\Large \dfrac{x}{1}=\dfrac{y-6}{-2}=\dfrac{z-6}{2}$

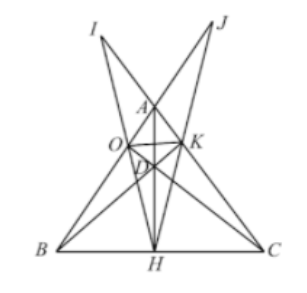
Ta có tứ giá BOKC là tứ giác nội tiếp đường tròn (vì có hai góc vuông K, O cùng nhìn BC dưới một góc vuông) suy ra $\Large \widehat{OKB}=\widehat{OCB}(1)$

Ta có tứ giác KDHC là tứ giác nội tiếp đường tròn (vì có hai góc vuông K, H cùng nhìn DC dưới một góc vuông) suy ra $\Large \widehat{DKH}=\widehat{OCB}(2)$

Từ (1) và (2) suy ra $\Large \widehat{DKB}=\widehat{OKB}$. Do đó BK là đường phân giác trong của góc $\Large \widehat{OKH}$ và AC là đường phân giác ngoài của góc $\Large \widehat{OKH}$

Tương tự ta chứng minh được OC là đường phân giác trong của góc $\Large \widehat{KOH}$ và AB là đường phân giác ngoài của góc $\Large \widehat{KOH}$

Ta cso $\Large OK=4,OH=3,KH=5$

Gọi I, J lần lượt là chân đường phân giác ngoài của góc $\Large \widehat{OKH}$ và $\Large \widehat{KOH}$

Ta có $\Large I=AC\cap HO$ ta có $\Large \dfrac{IO}{IH}=\dfrac{KO}{KH}=\dfrac{4}{5}\Rightarrow \overrightarrow{IO}=\dfrac{4}{5}\overrightarrow{IH}\Rightarrow I(-8;-8;-4)$

Ta có $\Large J=AB\cap KH$ ta có $\Large \dfrac{JK}{JH}=\dfrac{OK}{OH}=\dfrac{4}{3}\Rightarrow \overrightarrow{JK}=\dfrac{4}{3}\overrightarrow{JH}\Rightarrow J(16;4;-4)$

Đường thẳng IK qua I nhận $\Large \overrightarrow{IK}=\left(\dfrac{16}{3};\dfrac{28}{3};\dfrac{20}{3}\right)=\dfrac{4}{3}(4;7;5)$ làm vecto chỉ phương có phương trình $\Large (IK):\left\{\begin{align}&x=-8+4t\\&y=-8+7t\\&z=-4+5t\\\end{align}\right.$

Đường thẳng OJ qua O nhận $\Large \overrightarrow{OJ}-(16;4;-4)=4(4;1;-1)$ làm vecto chỉ phương có phương trình $\Large (OJ):\left\{\begin{align}x=4t'\\&y=t'\\&z=t'\\\end{align}\right.$

Khi đó $\Large A=IK\cap OJ$, giải hệ ta tìm được $\Large A(-4;-1;1)$

Ta có $\Large \overrightarrow{IA}=(4;7;5)$ và $\Large \overrightarrow{IJ}=(24;12;0)$, ta tính $\Large \left[\overrightarrow{IA},\overrightarrow{IJ}\right]=(-60;120;-120)=-60(1;-2;2)$

Khi đó đường thẳng đi qua A và vuông góc với mặt phẳng (ABC) có vecto chỉ phương $\Large \overrightarrow{u}=(1;-2;2)$ nên có phương trình $\Large \dfrac{x+4}{1}=\dfrac{y+1}{-2}=\dfrac{z-1}{2}$