Trong không gian $\Large Oxyz$ cho mặt cầu $\Large (S):(x-1)^{2}+(y+2)

Trong không gian $\Large Oxyz$ cho mặt cầu $\Large (S):(x-1)^{2}+(y+2)^{2}+(z-3)^{2}=27$. Gọi $\Large (\alpha)$ là mặt phẳng đi qua 2 điểm $\Large A(0;0;-4);B(2;0;0)$ và cắt $\Large (S)$ theo giao tuyến là đường tròn $\Large (C)$ sao cho khối nón có đỉnh là tâm của $\Large (S)$, là hình tròn $\Large (C)$ có thể tích lớn nhất. Biết mặt phẳng $\Large (\alpha)$ có phương trình dạng $\Large ax+by-z+c=0$, khi đó $\Large a-b+c$ bằng:

• A. 2
• B. -4
• C. 8
• D. 0

+ Vì $\Large (\alpha)$ qua A ta có: $\Large -(-4)+c=0\rightarrow c= -4$

+ Vì $\Large (\alpha)$ qua B ta có $\Large 2a+c=0\Rightarrow a =2$

$\Large \Rightarrow (\alpha):2x+by-z-4=0$

+ Mặt cầu $\Large (S)$ có tâm $\Large I(1;-2;3),R=3\sqrt{3}$

+ Chiều cao khối nón: $\Large h=d_{(I,\alpha)}=\dfrac{|2-2b-3-4|}{\sqrt{4+b^{2}+1}}=\dfrac{|2b+5|}{\sqrt{b^{2}+5}}$

+ Bán kính đường tròn $\Large (C):r=\sqrt{R^{2}-h^{2}}=\sqrt{27-\left(\dfrac{|2b+5|}{\sqrt{b^{2}+5}}\right)^{2}}=\sqrt{27-\dfrac{(2b+5)^{2}}{b^{2}+5}}$

Thể tích khối nón $\Large V=\dfrac{1}{3}\pi r^{2}h=\dfrac{1}{3}\pi \left(27-\dfrac{(2b+5)^{2}}{b^{2}+5}\right)\dfrac{|2b+5|}{\sqrt{b^{2}+5}}$

+ Tới đây ta làm tự luận như sau:

Đặt $\Large t=\dfrac{|2b+5|}{\sqrt{b^{2}+5}}$ và xét hàm số $\Large f(t)=(27-t^{2})t$ trên đoạn $\Large [0;3\sqrt{3}]$

Ta có: $\Large f'(t)=27-3t^{2};f'(t)=0$ $\Large \Leftrightarrow \left[\begin{align}&t=3\\&t=-3(l)\\\end{align}\right.$ Ta có bảng biến thiên

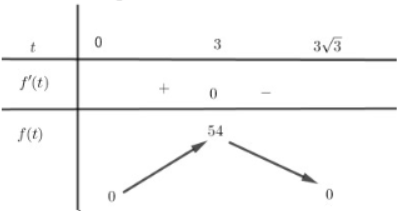
Do đó thể tích khối nón lớn nhất khi và chỉ khi

$\Large t=3\Leftrightarrow \left(\dfrac{|2b+5|}{\sqrt{b^{2}+5}}\right)^{2}=3^{2}\Leftrightarrow 4b^{2}+20b+25=9b^{2}+45%$

$\Large \Leftrightarrow 5b^{2}-20b^{2}+20=0\Leftrightarrow b =2$

Vì vậy $\Large a-b+c=-4$

Hoặc ta gọi chiều cao khối nón là h, từ phương trình tính thể tích ta suy ra h = 3, tìm b từ phương trình $\Large \dfrac{|2b+5|}{\sqrt{b^{2}+5}}=3$