Trong không gian với hệ tọa độ $\Large Oxy$, cho hình hộp chữ nhật $\L

Trong không gian với hệ tọa độ $\Large Oxy$, cho hình hộp chữ nhật $\Large ABCD.A'B'C'D'$ có A trùng với gốc tọa độ O, các đỉnh $\Large B(m;0;0), D(0;m;0), A'(0;0;n)$ với $\Large m,n>0$ và $\Large m+n=4$. Gọi M là trung điểm của cạnh CC'. Khi đó thể tích tứ diện $\Large BDA'M$ đạt giá trị lớn nhất bằng

• A. $\Large \dfrac{245}{108}$
• B. $\Large \dfrac{9}{4}$
• C. $\Large \dfrac{64}{27}$
• D. $\Large \dfrac{75}{32}$

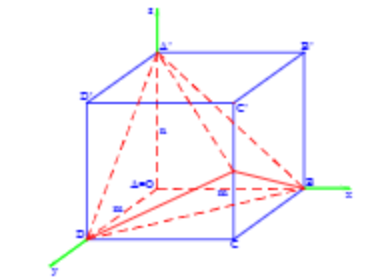
Tọa độ điểm $\Large C(m;m;0), C'(m;m;n), M\left(m;m;\dfrac{n}{2}\right)$

$\Large \overrightarrow{B'A}=(-m;0;n), \overrightarrow{BD}=(-m;m;0), \overrightarrow{BM}=\left(0;m;\dfrac{n}{2}\right)$

$\Large [\overrightarrow{BA'},\overrightarrow{BD}]=(-mn;-mm;m^{2})$

$\Large V_{BDA'M}=\dfrac{1}{6}|[\overrightarrow{BA'},\overrightarrow{BD}]\overrightarrow{BM}|=\dfrac{m^{2}n}{4}$

Ta có $\Large m.m.(2n)\leq \left(\dfrac{m+m+2n}{3}\right)^{3}=\dfrac{512}{27}\Rightarrow m^{2}n\leq \dfrac{256}{27}$

$\Large V_{BDA'M}\leq \dfrac{64}{27}$