Trong không gian Oxyz, cho mặt cầu (S) tâm I đi qua hai điểm ) và A(-4

Trong không gian Oxyz, cho mặt cầu (S) tâm I đi qua hai điểm ) và A(-4;0;4) sao cho tam giác OIA có diện tích bằng $\Large 2\sqrt{2}$. Khi đó diện tích mặt cầu (S) bằng

• A. $\Large 12\pi$
• B. $\Large 324\pi$
• C. $\Large 4\pi$
• D. $\Large 36\pi$

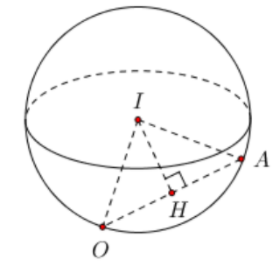
Gọi $\Large H(x_H;y_H;z_H)$ là giao điểm của OA

$\Large \Rightarrow \left\{\begin{align}&x_H=\dfrac{x_A+x_O}{2}=\dfrac{-4+0}{2}=-2\\&y_H=\dfrac{y_A+y_O}{2}=\dfrac{0+0}{2}=0\\&z_H=\dfrac{z_A+z_O}{2}=\dfrac{4+0}{2}=2\\\end{align}\right.$

$\Large \Rightarrow H(-2;0;2)$

Ta có

$\Large \overrightarrow{OA}=(-4;0;4)\Rightarrow OA=4\sqrt{2}$

$\Large \Rightarrow OH=\dfrac{1}{2}OA=2\sqrt{2}$
Do $\Large IA=IO\Rightarrow \Delta IOA$ cân tại $\Large I\Rightarrow IH\perp OA$

$\Large \Rightarrow IH=\dfrac{2S_{\Delta IOA}}{OA}=\dfrac{2.2\sqrt{2}}{4\sqrt{2}}=1$

$\Large \Rightarrow R=IO=\sqrt{IH^{2}+HO^{2}}=\sqrt{1^{2}+(2\sqrt{2})^{2}}=3$

$\Large \Rightarrow S=4\pi R^{2}=4\pi 3^{2}=36\pi$