Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi G là t

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi G là trọng tâm tam giác ABC. Tính theo a khoảng cách từ điểm G đến mặt phẳng (SCD)

• A. $\Large \dfrac{a\sqrt{6}}{9}$
• B. $\Large \dfrac{a\sqrt{6}}{3}$
• C. $\Large \dfrac{2a\sqrt{6}}{9}$
• D. $\Large \dfrac{a\sqrt{6}}{4}$

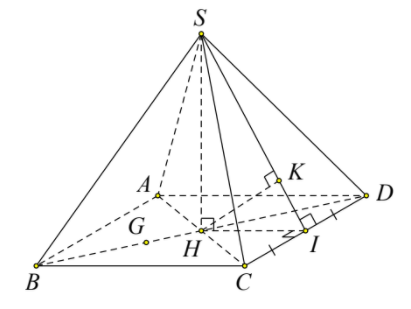Gọi I là trung điểm CD và H là tâm hình vuông ABCD

Ta có $\Large HI=\dfrac{a}{2};SH=\sqrt{SB^{2}-BH^{2}}=\sqrt{a^{2}-\left(\dfrac{a\sqrt{2}}{2}\right)^{2}}=\dfrac{a\sqrt{2}}{2}$

Xét tam giác vuông SHI ta có: $\Large \dfrac{1}{HK^{2}}=\dfrac{1}{SH^{2}}+\dfrac{1}{HI^{2}}=\dfrac{6}{a^{2}}\Rightarrow HK=\dfrac{a\sqrt{6}}{6}$

Gọi $\Large d_1=d(G,(SCD))$, ta có: $\Large \dfrac{HK}{d_1}=\dfrac{DH}{DG}=\dfrac{3}{4}\Rightarrow d_1=\dfrac{4}{3}HK=\dfrac{2a\sqrt{6}}{9}$