Gọi $\Large z_1,z_2$ là hai trong các số phức z thỏa mãn $\Large |z-3+

Gọi $\Large z_1,z_2$ là hai trong các số phức z thỏa mãn $\Large |z-3+5i|=5$ và $\Large |z_1-z_2|=6$. Tìm môđun của số phức $\Large w=z_1+z_2-6+10i$ 

• A. |w|=10
• B. |w|=32
• C. |w|=16
• D. |w|=8

Giả sử số phức z có dạng $\Large z=x+yi$

$\Large \Rightarrow |z-3+5i|^{2}=|z-(3-5i)|^{2}=(x-3)^{2}+(y+5)^{2}=5^{2}$

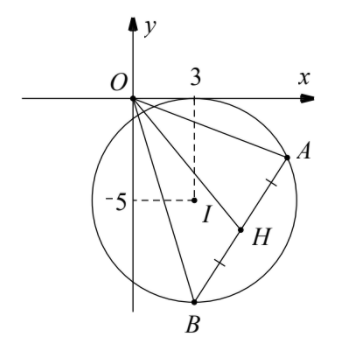
$\Large \Rightarrow z$ là tập hợp những số phức có tọa độ là những điểm thuộc đường tròn tâm I(3;-5) có bán kính R = 5. Gọi A, B lần lượt là điểm biểu diễn của $\Large z_1,z_2$ trên hệ trục tọa độ. Gọi H là trung điểm AB

Vì $\Large z_1-z_2=\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}\Rightarrow AB=|\overrightarrow{BA}|=|z_1-z_2|=6$

Ta có

$\Large w=z_1+z_2-6+10i=(z_1-(3-5i))+(z_2-(3-5i))=(\overrightarrow{OA}-\overrightarrow{OI})+(\overrightarrow{OB}-\overrightarrow{OI})=\overrightarrow{IA}+\overrightarrow{IB}=2\overrightarrow{OH}$

$\Large |w|=2|\overrightarrow{OH}|=2\sqrt{IA^{2}-AH^{2}}=2\sqrt{IA^{2}-\left(\dfrac{AB}{2}\right)^{2}}=8$