Cho hàm số $\Large y=f(x)=ax^{3}+bx^{2}+cx+d(a,b,c,d\in\mathbb{R})$ có

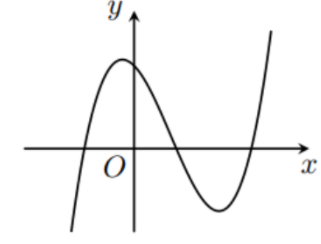
Cho hàm số $\Large y=f(x)=ax^{3}+bx^{2}+cx+d(a,b,c,d\in\mathbb{R})$ có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?

• A. $\Large a > 0, b > 0, c > 0, d < 0$
• B. $\Large a > 0, b > 0, c < 0, d < 0$
• C. $\Large a > 0, b < 0, c < 0, d > 0$
• D. $\Large a > 0, b < 0, c > 0, d > 0$

Xét các yếu tố:

+ Dáng điệu đồ thị $\Large \Rightarrow a > 0$

+ Đồ thị cắt trục tung tại điểm có tung độ dương nên $\Large d > 0$

+ Đồ thị có hai điểm cực trị hoành độ $\Large x_1,x_2$ và $\Large x_1+x_2 > 0$

Mà $\Large x_1,x_2$ là nghiệm của phương trình $\Large y'=3ax^{2}+2bx+c=0$ nên $\Large \left\{\begin{align}&P=\dfrac{c}{3a} < 0\\&S=-\dfrac{2b}{3a} > 0\\\end{align}\right.$

$\Large \Rightarrow \left\{\begin{align}&c < 0\\&b < 0\\\end{align}\right.$

Vậy ta có $\Large a > 0, b < 0, c < 0, d > 0$