Cho khối nón (N) có chiều cao h = 20cm, bán kính đáy r = 25 cm. Gọi $\

Cho khối nón (N) có chiều cao h = 20cm, bán kính đáy r = 25 cm. Gọi $\Large (\alpha)$ là mặt phẳng đi qua đỉnh của (N) và cách tâm của mặt đáy 12cm. Khi đó $\Large (\alpha)$ cắt (N) theo một thiết diện có diện tích là

• A. $\Large S=300cm^{2}$
• B. $\Large S=500cm^{2}$
• C. $\Large S=406cm^{2}$
• D. $\Large S=400cm^{2}$

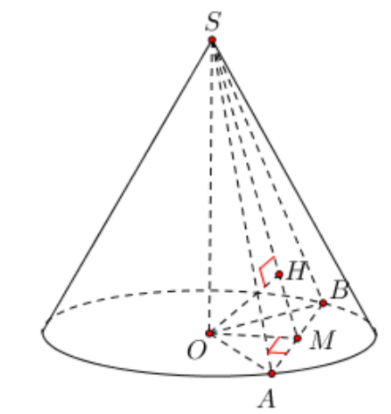Gọi M là trung điểm của AB

Ta có $\Large \left\{\begin{align}&AB\perp SO\\&AB\perp OM\\&SO\cap OM=\left\{O\right\}$ trong (SOM)

$\Large \Rightarrow AB\perp (SOM)$

Kẻ OH\perp SM$ tại H. Ta có $\Large \left\{\begin{align}&OH\perp SM\\&OH\perp AB(AB\perp (SOM),OH\sub(SOM))\Rightarrow OH\perp (SAB)\\&SM\cap AB=\left\{M\right\}trong(SAB)\\\end{align}\right.$

Do đó khoảng cách từ tâm của mặt đáy đến thiết diện bằng độ dài OH

Suy ra OH = 12cm

* Tính SM: Xét tam giác SOM vuông tại O có

$\Large \dfrac{1}{OH^{2}}=\dfrac{1}{SO^{2}}+\dfrac{1}{OM^{2}}\Rightarrow \dfrac{1}{OM^{2}}=\dfrac{1}{OH^{2}}-\dfrac{1}{SO^{2}}=\dfrac{1}{12^{2}}-\dfrac{1}{20^{2}}=\dfrac{1}{225}\Rightarrow OM=15(cm)$

$\Large SM=\dfrac{SO.OM}{OH}=\dfrac{20.15}{12}=25(cm)$

* Tính AB: Xtes tam giác OAM vuông tại M có

$\Large AM^{2}=OA^{2}-OM^{2}=25^{2}-15^{2}=400\Rightarrow AM=20(cm)\Rightarrow AB=2AM=2.20=40(cm)$

Vậy diện tích thiết diện là $\Large S=\dfrac{1}{2}SM.AB=\dfrac{1}{2}.25.40=500(cm^{2})$