Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc vớ

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, $\Large SA=a\sqrt{2}$. Gọi $\Large B', D'$ là hình chiếu của A lần lượt trên SB, SD. Mặt phẳng (AB'D') cắt SC tại C'. Thể tích khối chóp S.AB'C'D' là

• A. $\Large V=\dfrac{2a^{3}\sqrt{3}}{3}$
• B. $\Large V=\dfrac{2a^{2}\sqrt{3}}{3}$
• C. $\Large V=\dfrac{2a^{3}\sqrt{3}}{9}$
• D. $\Large V=\dfrac{2a^{3}\sqrt{2}}{9}$

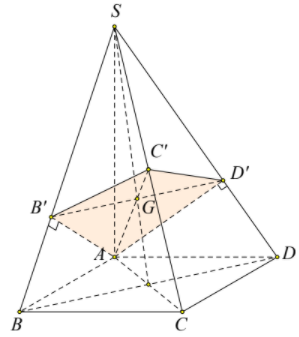
Ta có $\Large SB=\sqrt{SA^{2}+AB^{2}}=a\sqrt{3}$

Trong tam giác vuông SAB có $\Large SB'=\dfrac{SA^{2}}{SB}=\dfrac{2a\sqrt{3}}{3}\Rightarrow \dfrac{SB'}{SB}=\dfrac{2}{3}$

Gọi $\Large G=B'D'\cap AC'\Rightarrow G$ là trọng tâm tam giác $\Large SAC\Rightarrow C'$ là trung điểm của SC hay $\Large \dfrac{SC'}{SC}=\dfrac{1}{2}$

$\Large \dfrac{V_{S.AB'C'D'}}{S_{S.ABCD}}=\dfrac{2.V_{S.AB'C'}}{2.V_{S.ABC}}=\dfrac{V_{S.AB'C'}}{V_{S.ABC}}=\dfrac{SA}{SA}=\dfrac{SB'}{SB}=\dfrac{SC'}{SC}=\dfrac{2}{3}.\dfrac{1}{2}=\dfrac{1}{3}$

Mặt khác $\Large V_{S.ABC}=\dfrac{1}{3}S_{\Delta ABC}.SA=\dfrac{a^{3}\sqrt{2}}{6}\Rightarrow V_{S.AB'C'D'}=2.\left(\dfrac{1}{3}V_{S.ABC}\right)=\dfrac{a^{3}\sqrt{3}}{9}$