Trong không gian Oxyz, cho điểm A(-1; 0; 4). Xét đường thẳng $\large \

Trong không gian Oxyz, cho điểm A(-1; 0; 4). Xét đường thẳng $\large \Delta$ thay đổi, song song với trục Ox và cách trục Ox một khoảng bằng 2. Khi khoảng cách từ A đến $\large \Delta$ lớn nhất, $\large \Delta$ thuộc mặt phẳng nào dưới đây?

• A.

  $\large x + y + z - 2 = 0$

• B.

  $\large x + y  - 6z - 12 = 0$

• C.

  $\large y + z - 2 = 0$

• D.

  $\large y  - 6z - 12 = 0$

Cách 1:
Phương trình đường thẳng $\large \Delta$ song song với trục Ox $\large \left\{\begin{matrix} x = t \\ y = b \\ z = c \end{matrix}\right. (t \in \mathbb{R})$ đi qua M(0;b;c)
Khoảng cách giữa $\large \Delta$ và trục Ox là $\large d(\Delta;Ox) = \dfrac {\left | [\vec OM, \vec i] \right |}{\left | \vec i \right |} = \sqrt {b^{2} + c^{2}} = 2$
$\large \Leftrightarrow b^{2} + c^{2} = 4$       ($\large \vec i (1;0;0))$
Khoảng cách từ A(-1;0;4) đến $\large \Delta$ là $\large d(A; \Delta) =  \dfrac {\left | [\vec AM, \vec i] \right |}{\left | \vec i \right |} = \sqrt {b^{2} + (c - 4)^{2}} = \sqrt {4 - c^{2} + (c - 4)^{2}} = \sqrt {20 - 8c} \leq 6$ (do $\large -2 \leq c \leq 2$)
Dấu bằng xảy ra khi $\large \left\{\begin{matrix} c = -2 \\ b = 0 \end{matrix}\right.$. Phương trình đường thẳng $\large \Delta  \left\{\begin{matrix} x = t \\ y = 0 \\ z = -2 \end{matrix}\right.$ dễ thấy $\large \Delta$ thuộc mặt phẳng $\large y  - 6z - 12 = 0$
Cách 2:

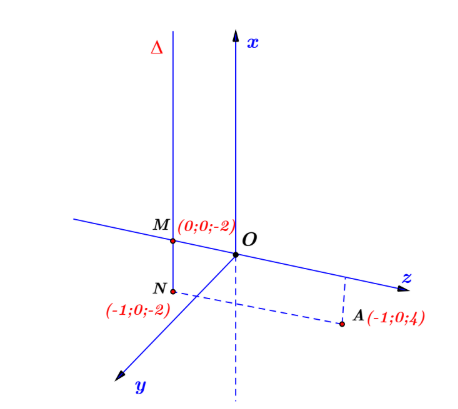
$\large d(A, \Delta)_{max} = 8$ khi $\large \Delta$ đi qua điểm M(0;0;-2) và N(-1;0;2)