Cho hàm số $\large y = f(x)$ liên tục trên có đạo hàm $\large y = f'(x

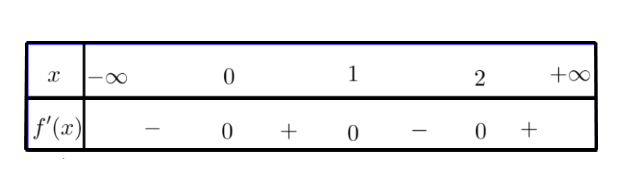
Cho hàm số  $\large y = f(x)$ liên tục trên có đạo hàm $\large y = f'(x)$ liên tục trên $\large \mathbb{R}$ và có bảng xét dấu như hình vẽ bên

Hỏi hàm số $\large y = f(x - 2 \left | x \right |)$ có tất cả bao nhiêu điểm cực trị

• A.

  4

• B.

  7

• C.

  9

• D.

  11

Tập xác định của hàm số $\large D = \mathbb{R}$
$\large y = h(x) = f(\left | x \right |^{2} - 2 \left | x \right |)$
$\large y' = h'(x) = f'(\left | x \right |^{2} - 2 \left | x \right |). \dfrac {x}{\left | x \right |}. (2 \left | x \right | -2)$
$\large h'(x) = 0 \Leftrightarrow$ $\large \Leftrightarrow \left[\begin{align}  &x = 1 \\ &x = -1 \\ &\left | x \right |^{2} - 2 \left | x \right | = 0 \\& \left | x \right |^{2} - 2 \left | x \right | = 1 \\ &\left | x \right |^{2} - 2 \left | x \right | = 2 \end{align}\right.$ $\large \Leftrightarrow \left[\begin{align} &x = 1 \\ &x = -2 \\ &x = 2 \\ &x = -2 \\ &x = 1 + \sqrt {2} \\ &x = - 1  - \sqrt {2} \\ &x = 1 + \sqrt {3} \\ &x = -1 - \sqrt {3} \end{align}\right.$
Ta thấy phương trình $\large h'(x) = 0$ có 8 nghiệm đơn (1) 
$\large h'(x)$ không tồn tại x = 0 mà x = 0 thuộc tập xác định đồng thời qua đó $\large h'(x)$ đổi dấu (2) 
Từ (1) và (2) suy ra hàm số đã cho có 8 điểm cực trị