Cho hàm số trùng phương $\large y = ax^{4} + bx^{2} + c$ có đồ thị như

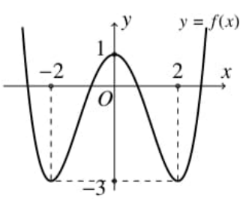
Cho hàm số trùng phương $\large y = ax^{4} + bx^{2} + c$ có đồ thị như hình vẽ. Hỏi đồ thị hàm số $\large y = \dfrac {(x^{2} - 4)(x^{2} + 2x)}{[f(x)]^{2} + 2f(x) - 3}$ có tổng cộng bao nhiêu tiệm cận đứng? 

• A.

  5

• B.

  2

• C.

  4

• D.

  3

$\large y = \dfrac {(x^{2} - 4)(x^{2} + 2x)}{[f(x)]^{2} + 2f(x) - 3} = \dfrac {x(x + 2)^{2}(x -2)}{[f(x)]^{2} + 2f(x) - 3}$
Ta có $\large [f(x)]^{2} + 2f(x) - 3 \Leftrightarrow \left[\begin{align} &f(x)=1 \\ &f(x)=-3 \end{align}\right.$ $\large \Leftrightarrow \left[\begin{align} &x = m (m < -2) \\ &x = 0 \\ &x = n (n > 2) \\ &x = 2 \\ &x=-2 \end{align}\right.$
Dựa vào đồ thị ta thấy các nghiệm $\large x = 0; x = \pm 2$ là các nghiệm kép (nghiệm bội 2) và đa thức $\large [f(x)]^{2} + 2f(x) - 3$ có bậc 8 nên $\large y = \dfrac{x(x + 2)^{2}(x -2)}{a^{2}x^{2}(x + 2)^{2}(x - 2)^{2}(x -m)(x - n)}$
Vậy hàm số có các tiệm cận đứng là $\large x = 0; x = 2; x = m; x = n$